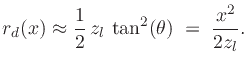Next |
Prev |
Up |
Contents |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider a spherical secondary source (``point source'')
located at
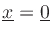 as shown in Fig.15. Then the
pressure amplitude along the listening line
as shown in Fig.15. Then the
pressure amplitude along the listening line
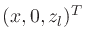 for all
for all 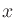 is given by
is given by
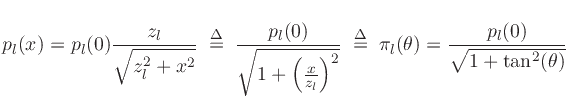 |
(9) |
where 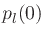 denotes the pressure amplitude observed from the point
source at
denotes the pressure amplitude observed from the point
source at
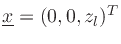 , and
, and
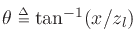 denotes the angle of the line from the source center to the line-array
point at
denotes the angle of the line from the source center to the line-array
point at 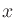 , i.e.,
, i.e.,
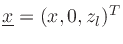 . This polar-pattern slice is
plotted in Fig.16 for the triangular
array+listener geometry such as described in §4.10 on page
. This polar-pattern slice is
plotted in Fig.16 for the triangular
array+listener geometry such as described in §4.10 on page ![[*]](../icons/crossref.png) , with
, with
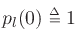 . The top plot shows
. The top plot shows 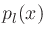 over a 12 m width
centered about a 6 m wide array, and the bottom plot shows
over a 12 m width
centered about a 6 m wide array, and the bottom plot shows
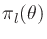 for
for
![$ \theta\in[-\pi/2,\pi/2]$](img206.png) , thereby covering the
entire axis containing array.
, thereby covering the
entire axis containing array.
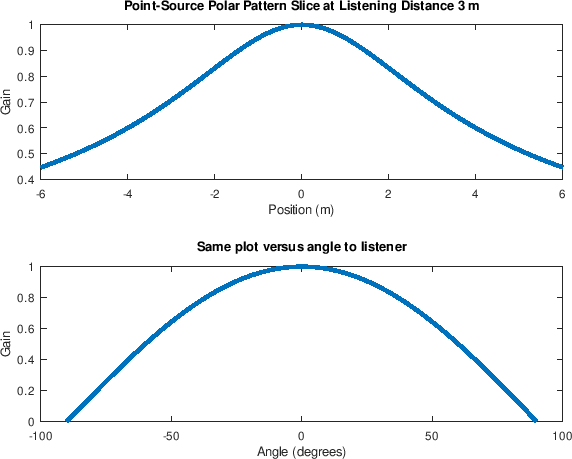
Figure 16:
Point-source
polar-pattern slice for a listening-line
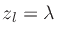 away from the
source. Top: Gain
away from the
source. Top: Gain 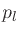 versus position
versus position 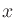 . Bottom: Gain
. Bottom: Gain 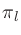 versus angle
versus angle
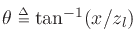 .
.
|
|
In addition to the gain variation 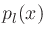 in Eq.(9), we also
have phase effects that we don't have when keeping radius
in Eq.(9), we also
have phase effects that we don't have when keeping radius 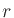 constant and only varying
constant and only varying 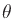 . The envelope
. The envelope 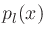 in Fig.16 is due only to spherical
spreading loss according to
in Fig.16 is due only to spherical
spreading loss according to 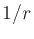 . The difference in propagation
distance between
. The difference in propagation
distance between 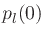 and
and 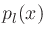 is
is
![$\displaystyle r_d(x) \isdef r_l(x)-r_l(0) = r_l(x)-z_l = \sqrt{z_l^2+x^2}-z_l = z_l\left[\sqrt{1+\tan^2(\theta)}-1\right]. \protect$](img208.png) |
(10) |
The resulting frequency-response
re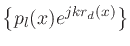 is
plotted in Fig.17 for 1 kHz (wavelength about a
foot (1.126 ft)) and
is
plotted in Fig.17 for 1 kHz (wavelength about a
foot (1.126 ft)) and 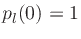 , where
, where
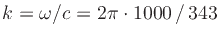 is the wavenumber (spatial radian frequency), which has
made its appearance for the first time in these formulas.34
is the wavenumber (spatial radian frequency), which has
made its appearance for the first time in these formulas.34
Figure 17:
Real part of point-source
frequency-response for a listening-line one wavelength away
(
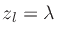 ). Top: Gain
). Top: Gain 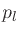 versus position
versus position 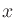 . Bottom: Gain
. Bottom: Gain
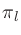 versus angle
versus angle
 .
.
|
|
For small  , we can use the approximation
, we can use the approximation
Next |
Prev |
Up |
Contents |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download huygens.pdf
[Comment on this page via email]
![]() as shown in Fig.15. Then the
pressure amplitude along the listening line
as shown in Fig.15. Then the
pressure amplitude along the listening line
![]() for all
for all ![]() is given by
is given by
![]() in Eq.(9), we also
have phase effects that we don't have when keeping radius
in Eq.(9), we also
have phase effects that we don't have when keeping radius ![]() constant and only varying
constant and only varying ![]() . The envelope
. The envelope ![]() in Fig.16 is due only to spherical
spreading loss according to
in Fig.16 is due only to spherical
spreading loss according to ![]() . The difference in propagation
distance between
. The difference in propagation
distance between ![]() and
and ![]() is
is

![]() , we can use the approximation
, we can use the approximation