Overlap-Add of Point-Source Frequency Responses

The listening point receives a sum of the radiating point-sources along the array. For an incident plane-wave traveling toward the listener, the sources are all ``in phase'', emitting identical signals. Let's focus on two adjacent sources for this case.

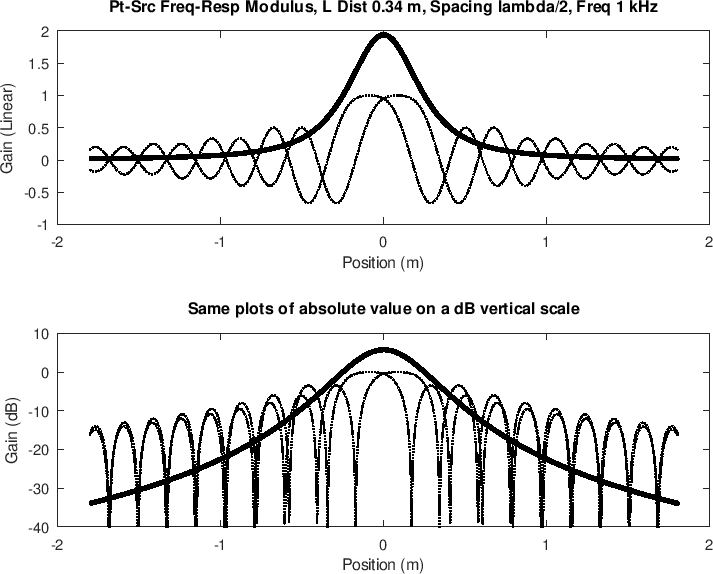
Figure 18 shows the magnitude of the sum of two identical point-sources separated by half a wavelength, and observed along a listening line one wavelength away from the two-source line array. Also shown is an overlay of the real parts of the component point-sources being summed, as in Fig.17. Notice how the pressure sums coherently near the center, but largely cancels far away from the center, especially to the far left and right where the half-wavelength spacing of the sources leads to almost complete cancellation.

Figure 18: Point-source frequency-response real parts and overlap-add magnitude, for two sources separated by half a wavelength ( $\approx 17$ cm), with the listening-line one wavelength away.

Consider now a larger array spanning 6 meters centered within a 12 m listening line, again one wavelength away. Figure 19(a) shows the OverLap-Add (OLA) result for the point-source frequency-response of Fig.17, again using source-separation $\lambda/2 \approx 17.2$    cm$\approx 6.76$    in , corresponding to ``critical sampling'' for extreme stage angles $\pm\pi/2$ at 1 kHz. The Gibbs phenomenon is highly visible, strongly suggesting a tapering window to reduce array truncation effects (§2.14). Tapering sinusoidally to zero (Hann half-windows) over 3 wavelengths (6 source points) produces the result shown in Fig.19(b). The normalized driving amplitude from each source is indicated by a small black circle.³⁵