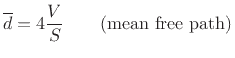Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A rough guide to the average delay-line length is the ``mean free
path'' in the desired reverberant environment. The mean free
path is defined as the average distance a ray of sound travels before
it encounters an obstacle and reflects. An approximate value for the
mean free path, due to Sabine, an early pioneer of statistical room
acoustics, is
where 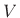 is the total volume of the room, and
is the total volume of the room, and  is total surface
area enclosing the room. This approximation requires the
diffuse field assumption, i.e., that plane waves are traveling
randomly in all directions [352,47] (see §3.2.1
for a simple construction). Normally, late reverberation satisfies
this assumption well, away from open doors and windows, provided the
room is not too ``dead''. Regarding each delay line as a
mean-free-path delay, the average can be set to the mean free path by
equating
is total surface
area enclosing the room. This approximation requires the
diffuse field assumption, i.e., that plane waves are traveling
randomly in all directions [352,47] (see §3.2.1
for a simple construction). Normally, late reverberation satisfies
this assumption well, away from open doors and windows, provided the
room is not too ``dead''. Regarding each delay line as a
mean-free-path delay, the average can be set to the mean free path by
equating
where 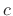 denotes sound speed and
denotes sound speed and 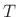 denotes the sampling period.
This number should be treated as a lower bound because in real rooms
reflections are often diffuse, especially at high frequencies.
In a diffuse reflection, a single incident plane wave reflects in many
directions at once.
denotes the sampling period.
This number should be treated as a lower bound because in real rooms
reflections are often diffuse, especially at high frequencies.
In a diffuse reflection, a single incident plane wave reflects in many
directions at once.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]