An interesting generalization of the single-input, single-output Schroeder allpass filter (defined in §2.8.1) was proposed by Gerzon [158] for use in artificial reverberation systems.
The starting point can be the first-order allpass of Fig.2.31a on
page ![]() , or the allpass made from two comb-filters depicted
in Fig.2.30 on
page
, or the allpass made from two comb-filters depicted
in Fig.2.30 on
page ![]() .3.15In either case,
.3.15In either case,
Let
![]() denote the
denote the ![]() input vector with components
input vector with components
![]() , and let
, and let
![]() denote
the corresponding vector of z transforms. Denote the
denote
the corresponding vector of z transforms. Denote the ![]() output
vector by
output
vector by
![]() . The resulting vector difference equation becomes,
in the frequency domain (cf. Eq.(2.15))
. The resulting vector difference equation becomes,
in the frequency domain (cf. Eq.(2.15))
which leads to the matrix transfer function
where
Note that to avoid implementing
![]() twice,
twice,
![]() should
be realized in vector direct-form II, viz.,
should
be realized in vector direct-form II, viz.,
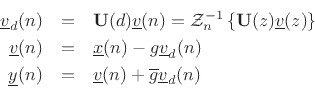
where ![]() denotes the unit-delay operator (
denotes the unit-delay operator (
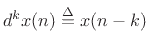 ).
).
To avoid a delay-free loop, the paraunitary matrix must include at
least one pure delay in every row, i.e.,
![]() where
where
![]() is paraunitary and causal.
is paraunitary and causal.
In [158], Gerzon suggested using
![]() of the form
of the form
where
Gerzon further suggested replacing the feedback and feedforward gains
![]() by digital filters
by digital filters ![]() having an amplitude response
bounded by 1. In principle, this allows the network to be arbitrarily
different at each frequency.
having an amplitude response
bounded by 1. In principle, this allows the network to be arbitrarily
different at each frequency.
Gerzon's vector Schroeder allpass is used in the IRCAM Spatialisateur [219].