Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Matrices
A matrix is defined as a rectangular array of numbers, e.g.,
which is a 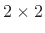 (``two by two'') matrix. A general matrix may
be
(``two by two'') matrix. A general matrix may
be  , where
, where 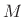 is the number of rows,
and
is the number of rows,
and 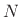 is the number of columns of the matrix.
For example, the general
is the number of columns of the matrix.
For example, the general 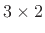 matrix is
matrix is
Either square brackets or large parentheses may be used to delimit the
matrix. The 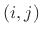 th elementH.1 of a matrix
th elementH.1 of a matrix
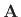 may be denoted by
may be denoted by
![$ \mathbf{A}[i,j]$](img2058.png) ,
,
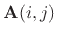 , or
, or
 . For example,
. For example,
![$ \mathbf{A}[1,2]=b$](img2061.png) in the
above two examples. The rows and columns of matrices are normally
numbered from
in the
above two examples. The rows and columns of matrices are normally
numbered from 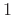 instead of from 0
; thus,
instead of from 0
; thus,
 and
and
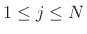 . When
. When  , the matrix is said to be
square.
, the matrix is said to be
square.
The transpose of a real matrix
 is denoted by
is denoted by
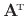 and is defined by
and is defined by
While
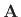 is
is  , its transpose is
, its transpose is  . We may
say that the ``rows and columns are interchanged'' by the transpose
operation, and transposition can be visualized as ``flipping'' the
matrix about its main diagonal. For example,
. We may
say that the ``rows and columns are interchanged'' by the transpose
operation, and transposition can be visualized as ``flipping'' the
matrix about its main diagonal. For example,
A complex matrix
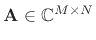 , is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
, is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
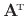 and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by
and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by 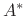 and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
Subsections
Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle \mathbf{A}= \left[\begin{array}{cc} a & b \\ [2pt] c & d \end{array}\right]
$](img2051.png)
![$\displaystyle \mathbf{A}= \left[\begin{array}{cc} a & b \\ [2pt] c & d \end{array}\right]
$](img2051.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right].
$](img2055.png)
![]() is denoted by
is denoted by
![]() and is defined by
and is defined by
![$\displaystyle \mathbf{A}^{\!\hbox{\tiny T}}[i,j] \isdef \mathbf{A}[j,i].
$](img2067.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right]^{\hbox{\tiny T}}
=\left[\begin{array}{ccc} a & c & e \\ b & d & f \end{array}\right].
$](img2069.png)
![]() , is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
, is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
![]() and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by
and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by ![]() and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
![$\displaystyle A^{\ast }[i,j] \isdef \overline{\mathbf{A}[j,i]}.
$](img2072.png)