Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider the linear system of equations
in matrix form:
This can be written in higher level form as
where
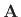 denotes the two-by-two matrix above, and
denotes the two-by-two matrix above, and
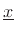 and
and
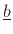 denote the two-by-one vectors. The solution to this equation
is then
denote the two-by-one vectors. The solution to this equation
is then
The general two-by-two matrix inverse is given by
and the inverse exists whenever 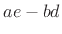 (which is called the determinant of the matrix
(which is called the determinant of the matrix
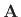 ) is nonzero. For larger matrices,
numerical algorithms are used to invert matrices, such as used by Matlab
based on LINPACK [26]. An initial introduction to matrices
and linear algebra can be found in [49].
) is nonzero. For larger matrices,
numerical algorithms are used to invert matrices, such as used by Matlab
based on LINPACK [26]. An initial introduction to matrices
and linear algebra can be found in [49].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
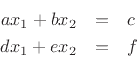
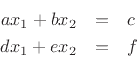
![$\displaystyle \left[\begin{array}{cc} a & b \\ [2pt] d & e \end{array}\right] \left[\begin{array}{c} x_1 \\ [2pt] x_2 \end{array}\right] = \left[\begin{array}{c} c \\ [2pt] f \end{array}\right]
$](img2106.png)
![$\displaystyle \underline{x}= \mathbf{A}^{-1}\underline{b}= \left[\begin{array}{cc} a & b \\ [2pt] d & e \end{array}\right]^{-1}\left[\begin{array}{c} c \\ [2pt] f \end{array}\right].
$](img2109.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ [2pt] d & e \end{array}\right]^{-1} = \frac{1}{ae-bd}\left[\begin{array}{cc} e & -b \\ [2pt] -d & a \end{array}\right]
$](img2110.png)