Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The Hermitian transpose of the general 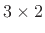 matrix is
matrix is
A column vector, e.g.,
is the special case of an 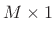 matrix,
while a row vector, e.g.,
matrix,
while a row vector, e.g.,
(as we have been using) is a 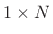 matrix. It is often helpful
to adopt the convention that all vectors written without the transpose
notation are column vectors, so that all row vectors require
the transpose notation, as in the equation above.
matrix. It is often helpful
to adopt the convention that all vectors written without the transpose
notation are column vectors, so that all row vectors require
the transpose notation, as in the equation above.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right]^{\ast }
=
\left[\begin{array}{ccc} \overline{a} & \overline{c} & \overline{e }\\
\overline{b} & \overline{d} & \overline{f }\end{array}\right].
$](img2073.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right]^{\ast }
=
\left[\begin{array}{ccc} \overline{a} & \overline{c} & \overline{e }\\
\overline{b} & \overline{d} & \overline{f }\end{array}\right].
$](img2073.png)
![$\displaystyle \underline{x}= \left[\begin{array}{c} x_0 \\ [2pt] x_1 \end{array}\right]
$](img2074.png)