Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The transfer function can be defined as the 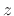 transform of
the impulse response:
transform of
the impulse response:
Using the closed-form sum of a matrix geometric series,G.4we obtain
 |
(G.5) |
Note that if there are 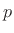 inputs and
inputs and 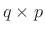 outputs,
outputs, 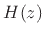 is a
is a 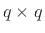 transfer-function matrix
(or ``matrix transfer function'').
transfer-function matrix
(or ``matrix transfer function'').
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() transform of
the impulse response:
transform of
the impulse response:
![$\displaystyle H(z) \isdef \sum_{n=0}^{\infty} h(n) z^{-n}
= D + \sum_{n=1}^{\infty} \left(C A^{n-1} B \right) z^{-n}
= D + z^{-1}C \left[\sum_{n=0}^{\infty} \left(z^{-1}A\right)^n\right] B
$](img2120.png)