Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Feedback Delay Networks (FDN)
Figure 2.28:
Order 3 MIMO Feedback Delay Network (FDN).
![\includegraphics[width=\twidth]{eps/FDNMIMO}](img529.png) |
The FDN can be seen as a vector feedback comb filter,3.10obtained by replacing the delay line with a diagonal delay matrix
(defined in Eq.(2.10) below), and replacing the feedback gain
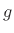 by the product of a diagonal matrix
by the product of a diagonal matrix
 times an orthogonal
matrix
times an orthogonal
matrix
 , as shown in
Fig.2.28 for
, as shown in
Fig.2.28 for 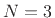 . The time-update for this FDN can be written
as
. The time-update for this FDN can be written
as
![$\displaystyle \left[\begin{array}{c} x_1(n) \\ [2pt] x_2(n) \\ [2pt] x_3(n)\end{array}\right] = \left[\begin{array}{ccc} g_1 & 0 & 0\\ [2pt] 0 & g_2 & 0\\ [2pt] 0 & 0 & g_3 \end{array} \right] \left[\begin{array}{ccc} q_{11} & q_{12} & q_{13}\\ [2pt] q_{21} & q_{22} & q_{23}\\ [2pt] q_{31} & q_{32} & q_{33} \end{array} \right] \left[\begin{array}{c} x_1(n-M_1) \\ [2pt] x_2(n-M_2) \\ [2pt] x_3(n-M_3)\end{array}\right] + \left[\begin{array}{c} u_1(n) \\ [2pt] u_2(n) \\ [2pt] u_3(n)\end{array}\right] \protect$](img533.png) |
(3.6) |
with the outputs given by
![$\displaystyle \left[\begin{array}{c} y_1(n) \\ [2pt] y_2(n) \\ [2pt] y_3(n)\end{array}\right] = \left[\begin{array}{c} x_1(n-M_1) \\ [2pt] x_2(n-M_2) \\ [2pt] x_3(n-M_3)\end{array}\right],$](img534.png) |
(3.7) |
or, in frequency-domain vector notation,
where
![$\displaystyle \mathbf{D}(z) \isdef \left[\begin{array}{ccc} z^{-M_1} & 0 & 0\\ [2pt] 0 & z^{-M_2} & 0\\ [2pt] 0 & 0 & z^{-M_3} \end{array} \right]. \protect$](img539.png) |
(3.10) |
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=\twidth]{eps/FDNMIMO}](img529.png)
![]() by the product of a diagonal matrix
by the product of a diagonal matrix
![]() times an orthogonal
matrix
times an orthogonal
matrix
![]() , as shown in
Fig.2.28 for
, as shown in
Fig.2.28 for ![]() . The time-update for this FDN can be written
as
. The time-update for this FDN can be written
as
![$\displaystyle \left[\begin{array}{c} y_1(n) \\ [2pt] y_2(n) \\ [2pt] y_3(n)\end{array}\right] = \left[\begin{array}{c} x_1(n-M_1) \\ [2pt] x_2(n-M_2) \\ [2pt] x_3(n-M_3)\end{array}\right],$](img534.png)