Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Delay Loop Expansion
When a subset of the resonating modes is nearly harmonically tuned,
it can be much more computationally efficient to use a filtered
delay loop (see §2.6.5) to generate an entire
quasi-harmonic series of modes rather than using a biquad for each
modal peak [443]. In this case, the resonator
model becomes
where 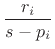 is the length of the delay line in the
is the length of the delay line in the 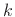 th comb filter,
and
th comb filter,
and 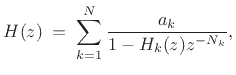 is a low-order filter which can be used to adjust finely
the amplitudes and frequencies of the resonances of the
is a low-order filter which can be used to adjust finely
the amplitudes and frequencies of the resonances of the 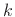 th comb
filter [432]. Recall (Chapter 6) that a single
filtered delay loop efficiently models a distributed 1D
propagation medium such as a vibrating string or acoustic tube. More
abstractly, a superposition of such quasi-harmonic mode series can
provide a computationally efficient psychoacoustic equivalent
approximation to arbitrary collections of modes in the range of
human hearing.
th comb
filter [432]. Recall (Chapter 6) that a single
filtered delay loop efficiently models a distributed 1D
propagation medium such as a vibrating string or acoustic tube. More
abstractly, a superposition of such quasi-harmonic mode series can
provide a computationally efficient psychoacoustic equivalent
approximation to arbitrary collections of modes in the range of
human hearing.
Note that when 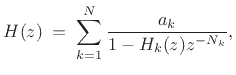 is close to
is close to 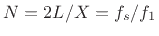 instead of
instead of 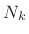 , primarily
only odd harmonic resonances are produced, as has been used in
modeling the clarinet [435].
, primarily
only odd harmonic resonances are produced, as has been used in
modeling the clarinet [435].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
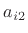
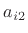
![]() is close to
is close to ![]() instead of
instead of ![]() , primarily
only odd harmonic resonances are produced, as has been used in
modeling the clarinet [435].
, primarily
only odd harmonic resonances are produced, as has been used in
modeling the clarinet [435].