Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Without damping, the ideal plucked string sounds more like a cheap
electronic organ than a string because the sound is perfectly periodic
and never decays. Static spectra are very boring to the ear. The
discrete Fourier transform (DFT) of the initial ``string loop''
contents gives the Fourier series coefficients for the periodic tone
produced.
The simplest change to the ideal wave equation of Eq.(6.1) that
provides damping is to add a term proportional to velocity:
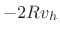 |
(7.14) |
Here, 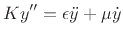 can be thought of as a very simple friction coefficient,
or resistance. As derived in §C.5, solutions to this wave
equation can be expressed as sums of left- and right-going
exponentially decaying traveling waves. When
can be thought of as a very simple friction coefficient,
or resistance. As derived in §C.5, solutions to this wave
equation can be expressed as sums of left- and right-going
exponentially decaying traveling waves. When 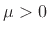 , we get
non-decaying traveling waves as before. As discussed in
§2.2.2, propagation losses may be introduced by the substitution
, we get
non-decaying traveling waves as before. As discussed in
§2.2.2, propagation losses may be introduced by the substitution
in each delay element (or wherever one sample of delay models one
spatial sample of wave propagation). By commutativity of LTI systems,
making the above substitution in a delay line of length 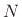 is
equivalent to simply scaling the output of the delay line by
is
equivalent to simply scaling the output of the delay line by 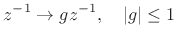 .
This lumping of propagation loss at one point along the
waveguide serves to minimize both computational cost and round-off
error. In general finite difference schemes, such a simplification is
usually either not possible or nonobvious.
.
This lumping of propagation loss at one point along the
waveguide serves to minimize both computational cost and round-off
error. In general finite difference schemes, such a simplification is
usually either not possible or nonobvious.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]