Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Fourier Series (FS) and Relation to DFT
In continuous time, a periodic signal 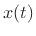 , with period
, with period 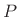 seconds,B.2 may be expanded
into a Fourier series with coefficients given by
seconds,B.2 may be expanded
into a Fourier series with coefficients given by
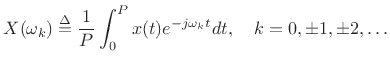 |
(B.5) |
where
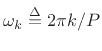 is the
is the 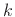 th harmonic frequency
(rad/sec). The generally complex value
th harmonic frequency
(rad/sec). The generally complex value
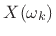 is called the
is called the
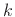 th Fourier series coefficient. The normalization by
th Fourier series coefficient. The normalization by 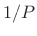 is optional, but often included to make the Fourier series
coefficients independent of the fundamental frequency
is optional, but often included to make the Fourier series
coefficients independent of the fundamental frequency 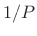 , and
thereby depend only on the shape of one period of the time
waveform.
, and
thereby depend only on the shape of one period of the time
waveform.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , with period
, with period ![]() seconds,B.2 may be expanded
into a Fourier series with coefficients given by
seconds,B.2 may be expanded
into a Fourier series with coefficients given by
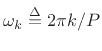 is the
is the