We now show that the DFT of a sampled signal ![]() (of length
(of length ![]() ),
is proportional to the
Fourier series coefficients of the continuous
periodic signal obtained by
repeating and interpolating
),
is proportional to the
Fourier series coefficients of the continuous
periodic signal obtained by
repeating and interpolating ![]() . More precisely, the DFT of the
. More precisely, the DFT of the ![]() samples comprising one period equals
samples comprising one period equals ![]() times the Fourier series
coefficients. To avoid aliasing upon sampling, the continuous-time
signal must be bandlimited to less than half the sampling
rate (see Appendix D); this implies that at most
times the Fourier series
coefficients. To avoid aliasing upon sampling, the continuous-time
signal must be bandlimited to less than half the sampling
rate (see Appendix D); this implies that at most ![]() complex harmonic components can be nonzero in the original
continuous-time signal.
complex harmonic components can be nonzero in the original
continuous-time signal.
If ![]() is bandlimited to
is bandlimited to
![]() , it can be sampled
at intervals of
, it can be sampled
at intervals of ![]() seconds without aliasing (see
§D.2). One way to sample a signal inside an integral
expression such as
Eq.(B.5) is to multiply it by a continuous-time impulse train
seconds without aliasing (see
§D.2). One way to sample a signal inside an integral
expression such as
Eq.(B.5) is to multiply it by a continuous-time impulse train
We wish to find the continuous-time Fourier series of the
sampled periodic signal ![]() . Thus, we replace
. Thus, we replace ![]() in
Eq.(B.5) by
in
Eq.(B.5) by
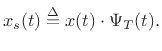
By the sifting property of delta functions (Eq.(B.4)), the Fourier series of
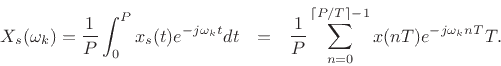
If the sampling interval ![]() is chosen so that it divides the signal
period
is chosen so that it divides the signal
period ![]() , then the number of samples under the integral is an integer
, then the number of samples under the integral is an integer
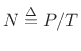 , and we obtain
, and we obtain
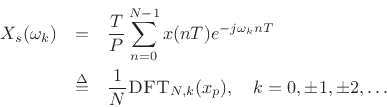
where
![$ x_p\isdef [x(0),x(T),\dots,x((N-1)T)]$](img1710.png) . Thus,
. Thus,
![]() for all
for all ![]() at which the bandlimited
periodic signal
at which the bandlimited
periodic signal ![]() has a nonzero harmonic. When
has a nonzero harmonic. When ![]() is odd,
is odd,
![]() can be nonzero for
can be nonzero for
![]() , while for
, while for
![]() even, the maximum nonzero harmonic-number range is
even, the maximum nonzero harmonic-number range is
![]() .
.
In summary,