Allpass Filters

This appendix addresses the general problem of characterizing all digital allpass filters, including multi-input, multi-output (MIMO) allpass filters. As a result of including the MIMO case, the mathematical level is a little higher than usual for this book. The reader in need of more background is referred to [84,37,98].

Our first task is to show that losslessness implies allpass.

Definition: A linear, time-invariant filter $H(z)$ is said to be lossless if it preserves signal energy for every input signal. That is, if the input signal is $x(n)$ , and the output signal is $y(n) = (h\ast x)(n)$ , then we have

$$\sum_{n=-\infty}^{\infty} \left\vert y(n)\right\vert^2 = \sum_{n=-\infty}^{\infty} \left\vert x(n)\right\vert^2.$$

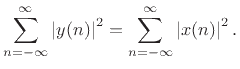
In terms of the $\ensuremath{L_2}$ signal norm $\left\Vert\,\,\cdot\,\,\right\Vert _2$ , this can be expressed more succinctly as

$$\left\Vert\,y\,\right\Vert _2^2 = \left\Vert\,x\,\right\Vert _2^2.$$

Notice that only stable filters can be lossless, since otherwise $\left\Vert\,y\,\right\Vert$ can be infinite while $\left\Vert\,x\,\right\Vert$ is finite. We further assume all filters are causal^C.1 for simplicity. It is straightforward to show the following:

Theorem: A stable, linear, time-invariant (LTI) filter transfer function $H(z)$ is lossless if and only if

$$\left\vert H(\ejo )\right\vert = 1, \quad \forall \omega.$$

That is, the frequency response must have magnitude 1 everywhere over the unit circle in the complex $z$ plane.

Proof: We allow the signals $x(n),y(n)$ and filter impulse response $h(n)$ to be complex. By Parseval's theorem [84] for the DTFT, we have,^C.2 for any signal $x\leftrightarrow X$ ,

$$\left\Vert\,x\,\right\Vert _2 = \left\Vert\,X\,\right\Vert _2$$

i.e.,

$$\left\Vert\,x\,\right\Vert _2^2 \isdef \sum_{n=-\infty}^\infty \left\vert x(n)\right\vert^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi} \left\vert X(\ejo )\right\vert^2 d\omega \isdef \left\Vert\,X\,\right\Vert _2^2.$$

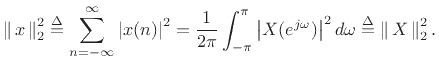
Thus, Parseval's theorem enables us to restate the definition of losslessness in the frequency domain:

$$\left\Vert\,X\,\right\Vert _2^2 = \left\Vert\,Y\,\right\Vert _2^2 = \left\Vert\,H\cdot X\,\right\Vert _2^2$$

where $Y=HX$ because the filter $H$ is LTI. Thus, $H$ is lossless by definition if and only if

$$\frac{1}{2\pi}\int_{-\pi}^{\pi} \left\vert X(\ejo )\right\vert^2 d\omega = \frac{1}{2\pi}\int_{-\pi}^{\pi} \left\vert H(\ejo )\right\vert^2\left\vert X(\ejo )\right\vert^2 d\omega. \protect$$ (C.1)

Since this must hold for all $X(\ejo )$ , we must have $\left\vert H(\ejo )\right\vert=1$ for all $\omega$ , except possibly for a set of measure zero (e.g., isolated points which do not contribute to the integral) [73]. If $H(z)$ is finite order and stable, $H(\ejo )$ is continuous over the unit circle, and its modulus is therefore equal to 1 for all $\omega\in[-\pi,\pi]$ . $\Box$

We have shown that every lossless filter is allpass. Conversely, every unity-gain allpass filter is lossless.