Theorem: A
To generalize lossless filters to the multi-input, multi-output (MIMO) case, we must generalize conjugation to MIMO transfer function matrices:
Theorem: A ![]() transfer function matrix
transfer function matrix
![]() is
lossless if and only if
its frequency-response matrix
is
lossless if and only if
its frequency-response matrix
![]() is unitary, i.e.,
is unitary, i.e.,

Let
![]() denote the length
denote the length ![]() output vector at time
output vector at time ![]() , and
let
, and
let
![]() denote the input
denote the input ![]() -vector at time
-vector at time ![]() . Then in the
frequency domain we have
. Then in the
frequency domain we have
![]() , which
implies
, which
implies
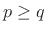
or
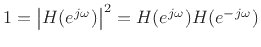
Integrating both sides of this equation with respect to
We have thus shown that in the MIMO case, losslessness is equivalent to having a unitary frequency-response matrix. A MIMO allpass filter is therefore any filter with a unitary frequency-response matrix.
Note that
![]() is a
is a ![]() matrix product
of a
matrix product
of a ![]() times a
times a ![]() matrix. If
matrix. If ![]() , then the rank
must be deficient. Therefore,
, then the rank
must be deficient. Therefore, ![]() . (There must be at least as
many outputs as there are inputs, but it's ok to have extra outputs.)
. (There must be at least as
many outputs as there are inputs, but it's ok to have extra outputs.)