An interesting property of allpass filters is that they can be
nested [415,153,154].
That is, if ![]() and
and
![]() denote unity-gain allpass transfer functions, then both
denote unity-gain allpass transfer functions, then both
![]() and
and
![]() are allpass filters. A proof can be
based on the observation that, since
are allpass filters. A proof can be
based on the observation that, since
![]() ,
, ![]() can
be viewed as a conformal map
[329] which maps the unit circle in the
can
be viewed as a conformal map
[329] which maps the unit circle in the ![]() plane to itself;
therefore, the set of all such maps is closed under functional
composition.
plane to itself;
therefore, the set of all such maps is closed under functional
composition.
An important class of nested allpass filters is obtained by nesting first-order allpass filters of the form
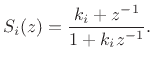
The nesting begins with
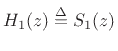 , and
, and
![$\displaystyle H_2(z) \isdef S_1\left([z^{-1}S_2(z)]^{-1}\right) \isdef \frac{k_1+z^{-1}S_2(z)}{1+k_1z^{-1}S_2(z)}.
$](img609.png)
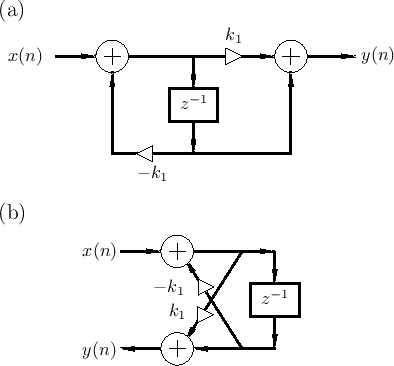
Figure 2.31a depicts the first-order allpass
The equivalence of nested allpass filters to lattice filters has computational significance since it is well known that the two-multiply lattice sections can be replaced by one-multiply lattice sections [299,317].
 |
![\includegraphics[width=4.45in]{eps/aptwo}](img612.png) |
In summary, nested first-order allpass filters are equivalent to lattice filters made of two-multiply lattice sections. In §C.8.4, a one-multiply section is derived which is not only less expensive to implement in hardware, but it additionally has a direct interpretation as a physical model.