Kelly-Lochbaum Scattering Junctions

Conservation of energy and mass dictate that, at the impedance discontinuity, force and velocity variables must be continuous

$$f_{i-1}(t,cT) = f_i(t,0)$$ (C.59)

$$v_{i-1}(t,cT) = v_i(t,0)$$

where velocity is defined as positive to the right on both sides of the junction. Force (or stress or pressure) is a scalar while velocity is a vector with both a magnitude and direction (in this case only left or right). Equations (C.57), (C.58), and (C.59) imply the following scattering equations (a derivation is given in the next section for the more general case of 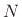$N$ waveguides meeting at a junction):

$$f^{{+}}_i(t) = \left[1+k_i(t) \right]f^{{+}}_{i-1}(t-T) - k_i(t) f^{{-}}_i(t)$$

$$f^{{-}}_{i-1}(t+T) = k_i(t)f^{{+}}_{i-1}(t-T) + \left[1-k_i(t)\right]f^{{-}}_i(t)$$ (C.60)

where

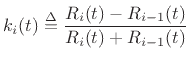$$k_i(t) \isdef \frac{ R_i(t)-R_{i-1}(t) }{R_i(t)+R_{i-1}(t) }$$ (C.61)

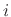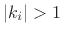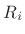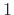is called the $i$ th reflection coefficient.^C.6 Since $R_i(t)\geq 0$ , we have $k_i(t)\in[-1,1]$ . It can be shown that if $\vert k_i\vert>1$ , then either $R_i$ or $R_{i-1}$ is negative, and this implies an active (as opposed to passive) medium. Correspondingly, lattice and ladder recursive digital filters are stable if and only if all reflection coefficients are bounded by $1$ in magnitude [299].

Figure C.20: The Kelly-Lochbaum scattering junction.

The scattering equations are illustrated in Figs. C.19b and C.20. In linear predictive coding of speech [485], this structure is called the Kelly-Lochbaum scattering junction, and it is one of several types of scattering junction used to implement lattice and ladder digital filter structures (§C.9.4,[299]).