Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Networks made up of connections of transmission-line like ``unit element'' filters, connected at scattering junctions.
- Originally conceived as a stable means of doing artificial reverberation, and modelling room acoustics.
- Impedances as well as line lengths may be time-varying, (audio effects, such as chorusing, flanging, etc.)
- Same passivity properties as circuit-based method (under finite arithmetic as well).
- a different point of view from the multi-D circuits: Begin in a discrete setting, no spectral mapping is used (explicitly).
- when applied to E+M problems, is roughly equivalent to TLM (Transmission Line Matrix method).
The Bidirectional Delay Line
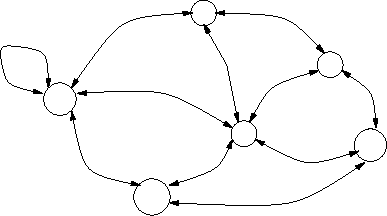
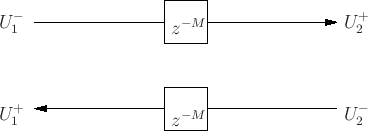
The central element in a digital waveguide network is a bidirectional delay line.
A bidirectional delay line has associated with it
- an impedance
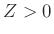 (
(
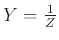 is the admittance
is the admittance
- a delay (usually an integer
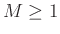 ) number of samples), same in both directions.
) number of samples), same in both directions.
- two incoming and outgoing (voltage) wave variables
- (optional) a physical length.
can be considered a discrete time lossless (LBR) two-port.(Indeed, it is included among the original wave digital filtering elements).
If the delay line pair has a physical length 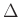 associated with it, then the two wave variables may be interpreted as travelling wave components which solve the 1D wave equation, where the speed is
associated with it, then the two wave variables may be interpreted as travelling wave components which solve the 1D wave equation, where the speed is
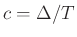 , and
, and 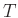 is the sample period.
is the sample period.
Traveling Wave Variables
We can define a related set of wave variables (current) in the bidirectional delay line by
for 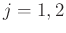 .
.
- sign inversion of incoming current wave with respect to outgoing (not left/right, but could be defined this way).
- current waves are auxiliary; need them only to define scattering junctions (not stored variables).
``Physical'' voltages and currents at the endpoints of the delay line pair:
for 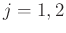 .
.
- A different formulation from MD wave digital filters: wave variables are instantaneously related to physical quantities (not to derivatives of them)
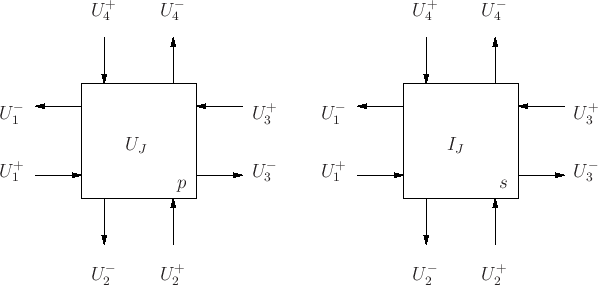
Scattering Junctions
Scattering Junctions (series and parallel) are defined identically to the WDF case.
Comments
- Passivity follows from power conservation at the junctions (Kirchoff's Laws) and LBR property of delay lines. No need to invoke MD-passivity, since we are dealing with, in a sense, lumped elements (unit element filters).
- Passivity under coefficient and signal truncation follows just as in WDF case.
- Generalizations include:
1D Transmission Line Revisited
The lossless source-free 1D transmission line equations are
Can apply centered differences over a uniform grid:
- Grid variables are staggered in time and space (Yee, FDTD).
Constant Parameters
If 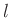 and
and 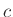 are constant, and we choose
are constant, and we choose
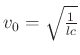 , then the difference equations simplify to a single equation in the voltages alone:
, then the difference equations simplify to a single equation in the voltages alone:
Just solving the wave equation, at the CFL limit.
Consider a chain of bidirectional delay lines, of length 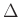 , and operating at time step
, and operating at time step 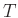 connected by parallel junctions:
connected by parallel junctions:
- Junction voltages solve the wave equation at CFL, if all impedances are identical (no scattering)
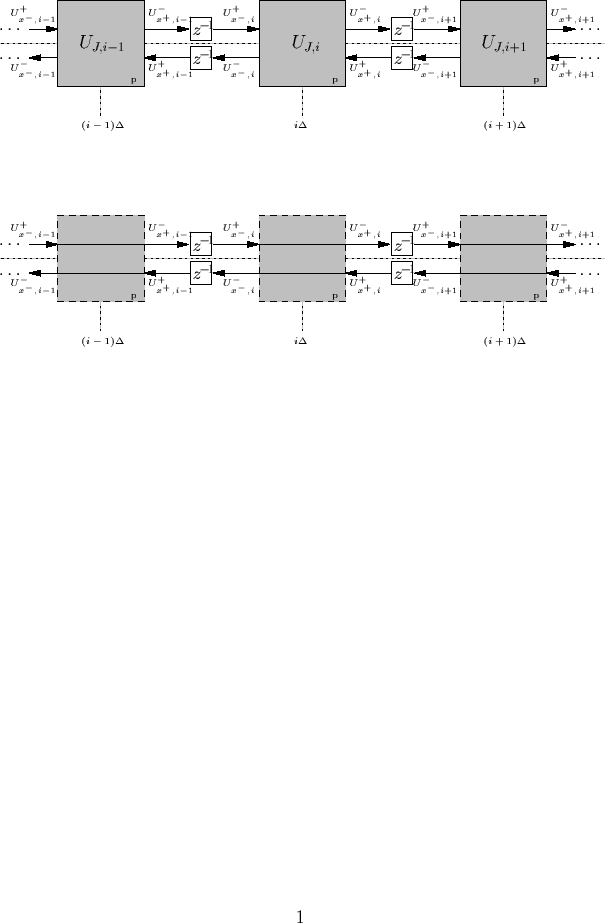
An Interleaved Mesh
Notice that it is possible to split a bidirectional delay line in the following way:
- Now have two half-sample, half-length delay lines of equal impedance (series junction functions, for the moment,as merely a sign inverter).
- Can employ this identity in the previous structure:
- Solves constant-parameter Transmission Line Equations, at CFL, on interleaved grid, if we choose
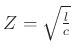 for all subsections.
for all subsections.
- Junction currents at series junctions give physical current.
Varying Material Parameters
Now we have 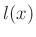 and
and 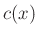 .
.
- Expect dispersion (scattering due to varying line impedance)
Natural fix: Delay line impedances should be different.
- Local propagation speed,
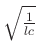 also varies
Fix: Insert passive ``storage'' registers at every junction, in order to slow down local propagation speed in mesh.
also varies
Fix: Insert passive ``storage'' registers at every junction, in order to slow down local propagation speed in mesh.
Examine a mesh of the following form:
- will solve T-line equations if line impedances chosen properly
- Get a family of difference methods, each with different stability properties.
- stability constraints derive from positivity condition on impedances (as per WDFs).
Losses and Sources
The full Transmission Line Equations are, including losses (resistive, and shunt conductive):
Can treat this by adding a ``resistive source'' (analogous to WDF counterpart) at every junction:
Simplifies considerably in certain cases...
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Meshes.pdf
Download Meshes_2up.pdf
Download Meshes_4up.pdf

![]() associated with it, then the two wave variables may be interpreted as travelling wave components which solve the 1D wave equation, where the speed is
associated with it, then the two wave variables may be interpreted as travelling wave components which solve the 1D wave equation, where the speed is
![]() , and
, and ![]() is the sample period.
is the sample period.
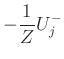
![]() matrix impedance
matrix impedance ![]() , with
, with ![]() .
.
![]() matrix reflectance
matrix reflectance ![]() ,
, ![]() paraunitary.
(comes in handy for solids, also as framework for treating TLM ``super-symmetric condensed node'')
paraunitary.
(comes in handy for solids, also as framework for treating TLM ``super-symmetric condensed node'')
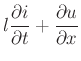
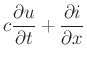
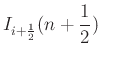
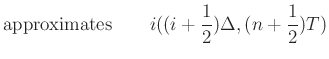

![]() and
and ![]() are constant, and we choose
are constant, and we choose
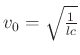 , then the difference equations simplify to a single equation in the voltages alone:
, then the difference equations simplify to a single equation in the voltages alone:
![]() , and operating at time step
, and operating at time step ![]() connected by parallel junctions:
connected by parallel junctions:


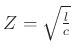 for all subsections.
for all subsections.
![]() and
and ![]() .
.

