Lumped vs. Distributed Systems

• A lumped system is one in which the dependent variables of interest are a function of time alone. In general, this will mean solving a set of ordinary differential equations (ODEs)

• A distributed system is one in which all dependent variables are functions of time and one or more spatial variables. In this case, we will be solving partial differential equations (PDEs)

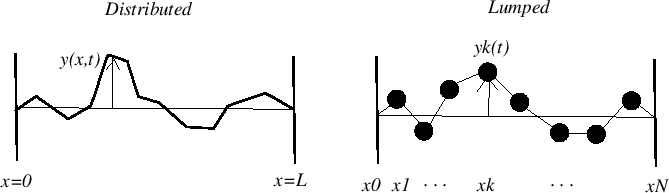
For example, consider the following two systems:

• The first system is a distributed system, consisting of an infinitely thin string, supported at both ends; the dependent variable, the vertical position of the string 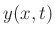$y(x,t)$ is indexed continuously in both space and time.

• The second system, a series of ``beads'' connected by massless string segments, constrained to move vertically, can be thought of as a lumped system, perhaps an approximation to the continuous string.

• For electrical systems, consider the difference between a lumped RLC network and a transmission line
  
  

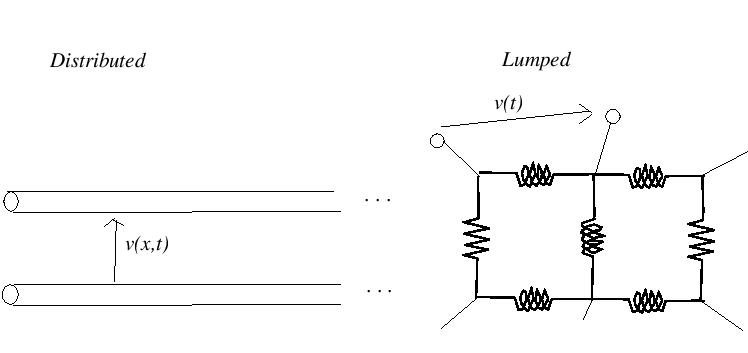
• The importance of lumped approximations to distributed systems will become obvious later, especially for waveguide-based physical modeling, because it enables one to cut computational costs by solving ODEs at a few points, rather than a full PDE (generally much more costly)