Transverse Motion of the Ideal Beam

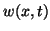Consider a thin beam, or rod, aligned parallel to the $x$ axis. We will be interested in the transverse motion of the beam, which we will assume to be restricted to one perpendicular direction; we will call the deflection of the beam from the $x$ axis $w(x,t)$. The relevant material parameters of the beam are the mass density 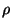$\rho$, the cross-sectional area 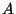$A$, Young's modulus 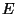$E$ and $I$, the moment of inertia of the beam about the perpendicular axis. The material parameters are, in general, allowed to be slowly-varying functions of $x$. 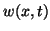Under the further assumptions that the beam deflection $w(x,t)$ is small, and that the beam cross-section remains perpendicular to the so-called ``neutral axis'', it is possible to arrive at the Euler-Bernoulli equation [77]:

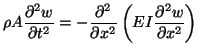$$\rho A \frac{\partial^{2}w}{\partial t^{2}} = -\frac{\partial^{2}}{\partial x^{2}}\left(EI\frac{\partial^{2}w}{\partial x^{2}}\right)$$ (5.1)

Notice that this equation contains a fourth order spatial derivative, resulting from the fact that the beam provides its own restoring stiffness, proportional to its curvature, in marked contrast to the equation for a string, which requires externally applied tension in order to support wave motion. In particular, it does not result from the elimination of variables in a hyperbolic system (see §3.2). If the material properties of the beam do not vary spatially, then (5.1) reduces to the more familiar form

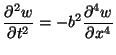$$\frac{\partial^{2}w}{\partial t^{2}} = -b^{2}\frac{\partial^{4}w}{\partial x^{4}}$$ (5.2)

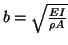where $b=\sqrt{\frac{EI}{\rho A}}$. In what follows, however, we will deal with the more general case.