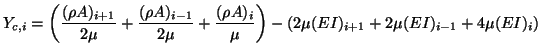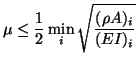Type II: Current-centered Network

This is the dual to the previous arrangement. Now we set

$$\tilde{Z}_{x^{-},i}=\tilde{Z}_{x^{+},i} = \frac{1}{2\mu (EI)_{i}}... ...0.5in}\tilde{Z}_{t,i} = \frac{1}{\mu (EI)_{i}}\hspace{0.5in}\tilde{Z}_{c,i} = 0$$

and we thus choose

$$Y_{c,i} = \left(\frac{(\rho A)_{i+1}}{2\mu}+\frac{(\rho A)_{i-1}}... ... A)_{i}}{\mu}\right)-\left(2\mu (EI)_{i+1}+2\mu (EI)_{i-1}+4\mu (EI)_{i}\right)$$

and we have the same stability condition as the previous case,

$$\mu\leq \frac{1}{2}\min_{i}\sqrt{\frac{(\rho A)_{i}}{(EI)_{i}}}$$