Fixed End, Allowed to Pivot

In this simple case, we have

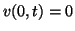$v(0,t)=0$ is ensured by terminating the parallel junction at 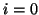$i=0$ with a short-circuit, so that 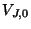$V_{J,0}$ is forced to zero. From Figure 5.4(a), we see that as a result (really by construction), we have 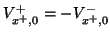$V_{x^{+},0}^{+} = -V_{x^{+},0}^{-}$. The second boundary condition, 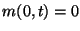$m(0,t) = 0$ can be enforced in a similar manner by terminating the series junction at grid location zero with an open circuit.