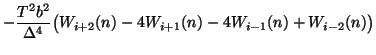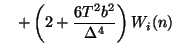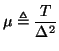Next: Waveguide Network for the
Up: Transverse Motion of the
Previous: Phase and Group Velocity
There are many ways to approach the numerical integration of (5.1). If the material parameters are constant, then a simple explicit method can be obtained by applying centered difference approximations to both the time and space derivatives, yielding the scheme
where 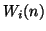 is a grid function defined for integer
is a grid function defined for integer  and
and  , and represents an approximation to
, and represents an approximation to
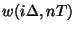 , where
, where  is a uniform grid spacing, and
is a uniform grid spacing, and 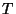 is the time step. This scheme is accurate to
is the time step. This scheme is accurate to
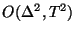 , but is stable only for
, but is stable only for
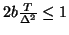 , so it is effectively only first-order accurate; this is typical of explicit methods for systems with some parabolic character [176].
, so it is effectively only first-order accurate; this is typical of explicit methods for systems with some parabolic character [176].
In order to deal more effectively with the varying-coefficient problem, we can divide (5.1) into a system of two PDEs, and differentiate with respect to time, to get
 |
(5.5a) |
Here,
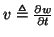 is the beam transverse velocity, and
is the beam transverse velocity, and 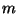 can be interpreted as a bending moment. We have chosen these variables in order to make clear the relationship of the classical beam theory with the more modern Timoshenko theory (see §5.2).
Applying centered differences to this system yields
can be interpreted as a bending moment. We have chosen these variables in order to make clear the relationship of the classical beam theory with the more modern Timoshenko theory (see §5.2).
Applying centered differences to this system yields
 |
(5.6a) |
where 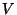 and
and  are the grid functions corresponding to
are the grid functions corresponding to 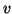 and
and 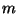 . Similarly to the case of the transmission line (see §4.3.6), we have used
. Similarly to the case of the transmission line (see §4.3.6), we have used
and in keeping with the literature [176], we have also defined
As for the transmission line, we can evaluate the grid functions 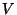 and
and  at alternating time steps. Due to the nature of the difference approximation, however, we cannot interleave these variables on the spatial grid. That is, we are forced to calculate both
at alternating time steps. Due to the nature of the difference approximation, however, we cannot interleave these variables on the spatial grid. That is, we are forced to calculate both 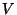 and
and  at every grid location (at their respective time steps). We have written the difference scheme above such that temporal interleaving is evident, i.e.
at every grid location (at their respective time steps). We have written the difference scheme above such that temporal interleaving is evident, i.e. 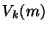 and
and 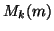 ,
, 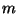 half-integer, are calculated only for (say)
half-integer, are calculated only for (say) 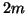 even and odd, respectively.
even and odd, respectively.



Next: Waveguide Network for the
Up: Transverse Motion of the
Previous: Phase and Group Velocity
Stefan Bilbao
2002-01-22