Phase and Group Velocity

Though equation (5.2) is not hyperbolic, it is simple to obtain a dispersion relationship by considering wave-like solutions of the form 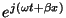$e^{j(\omega t + \beta x)}$, where 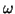$\omega$ is the frequency variable, and $\beta$ is the spatial wavenumber. The relationship can be written as

$$\omega^{2} - b^{2}\beta^{4} = 0$$

which has solutions

$$\omega = \pm b \beta^{2}$$

The phase and group velocities can then be written, from (3.12), as

$$\gamma_{EB}^{p} = \pm b\beta\hspace{1.0in}\gamma_{EB}^{g} = \pm 2b\beta$$

These velocities are now dependent on the spatial wavenumbers, and hence wave propagation is dispersive. Notice also that the group velocities are unbounded, so we will expect to run into some numerical difficulties (recall that for all the systems dealt with in the previous chapters, stability bounds on 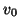$v_{0}$, the space step/time step ratio were dependent on a maximum group velocity).

We also mention that a good model for the piano string is based on the wave equation, and complemented by several perturbation terms, among which are a fourth spatial derivative term like the above [25]; such a term models frequency-dependent dispersion in the string.