The Second-Order Waveguide Filter

The first step is to make a second-order digital filter with zero damping by abutting two unit-sample sections of waveguide medium, and terminating on the left and right with perfect reflections, as shown in Fig.C.40. The wave impedance in section $i$ is given by $R_i=\rho c/A_i$ , where $\rho$ is air density, $A_i$ is the cross-sectional area of tube section $i$ , and $c$ is sound speed. The reflection coefficient is determined by the impedance discontinuity via $k=(R_1-R_2)/(R_1+R_2)$ . It turns out that to obtain sinusoidal oscillation, one of the terminations must provide an inverting reflection while the other is non-inverting.

Figure C.40: The second-order, lossless, digital waveguide oscillator, built using two acoustic tube sections.

At the junction between sections $1$ and $2$ , the signal is partially transmitted and partially reflected such that energy is conserved, i.e., we have lossless scattering. The formula for the reflection coefficient $k$ can be derived from the physical constraints that (1) pressure is continuous across the junction, and (2) there is no net flow into or out of the junction. For traveling pressure waves $p^\pm(t)$ and volume-velocity waves $u^\pm(t)$ , we have $p^+(t) = Ru^+(t)$ and $p^-(t) = -Ru^-(t)$ . The physical pressure and volume velocity are obtained by summing the traveling-wave components.

The discrete-time simulation for the physical system of Fig.C.40 is shown in Fig.C.41. The propagation time from the junction to a reflecting termination and back is one sample period. The half sample delay from the junction to the reflecting termination has been commuted with the termination and combined with the half sample delay to the termination. This is a special case of a ``half-rate'' waveguide filter [437].

Figure C.41: The second-order, lossless, waveguide filter.

Since only two samples of delay are present, the digital system is at most second order, and since the coefficients are real, at most one frequency of oscillation is possible in $(0,\pi)$ .

The scattering junction shown in the figure is called the Kelly-Lochbaum junction in the literature on lattice and ladder digital filters [174]. While it is the most natural from a physical point of view, it requires four multiplies and two additions for its implementation.

It is well known that lossless scattering junctions can be implemented in a variety of equivalent forms, such as the two-multiply and even one-multiply junctions. However, most have the disadvantage of not being normalized in the sense that changing the reflection coefficient $k$ changes the amplitude of oscillation. This can be understood physically by noting that a change in $k$ implies a change in $R_2/R_1$ . Since the signal power contained in a waveguide variable, say $p_1^+(n)$ , is $\left[p_1^+(n)\right]^2/R_1$ , we find that modulating the reflection coefficient corresponds to modulating the signal energy represented by the signal sample in at least one of the two delay elements. Since energy is proportional to amplitude squared, energy modulation implies amplitude modulation.

The well-known normalization procedure is to replace the traveling pressure waves $p^\pm$ by ``root-power'' pressure waves $\tilde{p}^\pm = p^\pm/\sqrt{R}$ so that signal power is just the square of a signal sample $(\tilde{p}^\pm)^2$ . When this is done, the scattering junction transforms from the Kelly-Lochbaum or one-multiply form into the normalized ladder junction in which the reflection coefficients are again $\pm k$ , but the forward and reverse transmission coefficients become $\sqrt{1-k^2}$ . Defining $k=\sin(\theta)$ , the transmission coefficients can be seen as $\cos(\theta)$ , and we arrive essentially at the coupled form, or two-dimensional vector rotation considered in [169].

An alternative normalization technique is based on the digital waveguide transformer (§C.16). The purpose of a ``transformer'' is to ``step'' the force variable (pressure in our example) by some factor $g$ without scattering and without affecting signal energy. Since traveling signal power is proportional to pressure times velocity $p^+u^+$ , it follows that velocity must be stepped by the inverse factor $1/g$ to keep power constant. This is the familiar behavior of transformers for analog electrical circuits: voltage is stepped up by the ``turns ratio'' and current is stepped down by the reciprocal factor. Now, since $p^+ = R u^+$ , traveling signal power is equal to $p^+u^+ = (p^+)^2/R$ . Therefore, stepping up pressure through a transformer by the factor $g$ corresponds to stepping up the wave impedance $R$ by the factor $g^2$ . In other words, the transformer raises pressure and decreases volume velocity by raising the wave impedance (narrowing the acoustic tube) like a converging cone.

If a transformer is inserted in a waveguide immediately to the left, say, of a scattering junction, it can be used to modulate the wave impedance ``seen'' to the left by the junction without having to use root-power waves in the simulation. As a result, the one-multiply junction can be used for the scattering junction, since the junction itself is not normalized. Since the transformer requires two multiplies, a total of three multiplies can effectively implement a normalized junction, where four were needed before. Finally, in just this special case, one of the transformer coefficients can be commuted with the delay element on the left and combined with the other transformer coefficient. For convenience, the $-1$ coefficient on the left is commuted into the junction so it merely toggles the signs of inputs to existing summers. These transformations lead to the final form shown in Fig.C.42.

Figure C.42: The transformer-normalized, digital waveguide oscillator.

The ``tuning coefficient'' is given by $C(n)=\cos(2\pi f_nT)$ , where $f_n$ is the desired oscillation frequency in Hz at sample $n$ (in the undamped case), and $T$ is the sampling period in seconds. The ``amplitude coefficient'' is $G(n) = r_n g_n/g_{n-1}$ , where growth or decay factor per sample ( $r_n\equiv 1$ for constant amplitude),^C.18 and $g_n$ is the normalizing transformer ``turns ratio'' given by

$$g_n=\sqrt{\frac{1-C(n)}{1+C(n)}}.$$

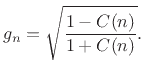
When both amplitude and frequency are constant, we have $G(n)\equiv 1$ , and only the tuning multiply is operational. When frequency changes, the amplitude coefficient deviates from unity for only one time sample to normalize the oscillation amplitude.

When amplitude and frequency are constant, there is no gradual exponential growth or decay due to round-off error. This happens because the only rounding is at the output of the tuning multiply, and all other computations are exact. Therefore, quantization in the tuning coefficient can only cause quantization in the frequency of oscillation. Note that any one-multiply digital oscillator should have this property. In contrast, the only other known normalized oscillator, the coupled form, does exhibit exponential amplitude drift because it has two coefficients $c=\cos(\theta)$ and $s=\sin(\theta)$ which, after quantization, no longer obey $c^2+s^2=1$ for most tunings.