We now consider filter banks with an arbitrary number of channels, and ask under what conditions do we obtain a perfect reconstruction filter bank?
Polyphase analysis will give us the answer readily.
Let's begin with the ![]() -channel filter bank below:
-channel filter bank below:
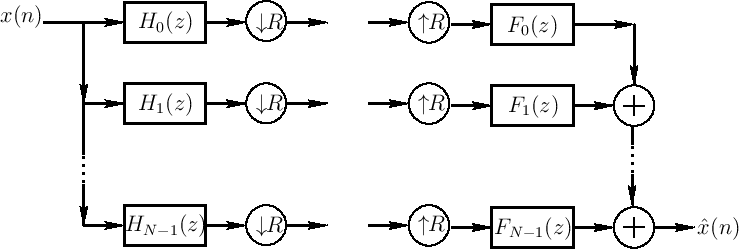
The next step is to expand each analysis filter ![]() into its
into its
![]() -channel ``Type 1'' polyphase representation:
-channel ``Type 1'' polyphase representation:
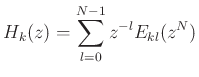
or
![$\displaystyle \underbrace{\left[\begin{array}{c} H_0(z) \\ [2pt] H_1(z) \\ [2pt] \vdots \\ [2pt] H_{N-1}(z)\end{array}\right]}_{\bold{h}(z)} =
\underbrace{\left[\begin{array}{cccc}
E_{0,0}(z^N) & E_{0,1}(z^N) & \cdots & E_{0,N-1}(z^N) \\
E_{1,0}(z^N) & E_{1,1}(z^N) & \cdots & E_{1,N-1}(z^N)\\
\vdots & \vdots & \cdots & \vdots\\
E_{N-1,0}(z^N) & E_{N-1,1}(z^N) & \cdots & E_{N-1,N-1}(z^N)
\end{array}\right]}_{\bold{E}(z^N)}
\underbrace{\left[\begin{array}{c} 1 \\ [2pt] z^{-1} \\ [2pt] \vdots \\ [2pt] z^{-(N-1)}\end{array}\right]}_{\bold{e}(z)}
$](img232.png)
which we can write as
Similarly, expand the synthesis filters in a Type II polyphase decomposition:
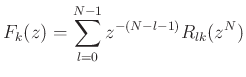
or
![$\displaystyle \underbrace{\left[\begin{array}{c} F_0(z) \\ [2pt] F_1(z) \\ [2pt] \vdots \\ [2pt] F_{N-1}(z)\end{array}\right]^T}_{\bold{f}^T(z)} =
\underbrace{\left[\begin{array}{c} z^{-(N-1)} \\ [2pt] z^{-(N-2)} \\ [2pt] \vdots \\ [2pt] 1\end{array}\right]^T}_{{\tilde{\bold{e}}}(z)}
\underbrace{\left[\begin{array}{cccc}
R_{0,0}(z^N) & R_{0,1}(z^N) & \cdots & R_{0,N-1}(z^N) \\
R_{1,0}(z^N) & R_{1,1}(z^N) & \cdots & R_{1,N-1}(z^N)\\
\vdots & \vdots & \cdots & \vdots\\
R_{N-1,0}(z^N) & R_{N-1,1}(z^N) & \cdots & R_{N-1,N-1}(z^N)
\end{array}\right]}_{\bold{R}(z^N)}
$](img235.png)
which we can write as
The polyphase representation can now be depicted as
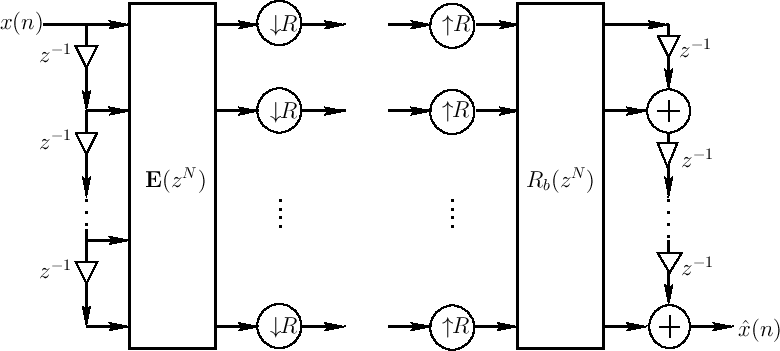
When ![]() , commuting the up/downsamplers gives
, commuting the up/downsamplers gives
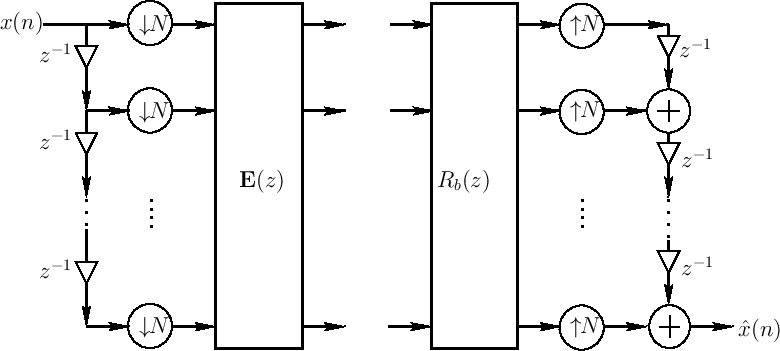
We call
![]() the polyphase matrix.
the polyphase matrix.
As we will show below, the above simplification can be carried out
more generally whenever ![]() divides
divides ![]() (e.g.,
(e.g.,
![]() ). In these cases
). In these cases
![]() becomes
becomes
![]() and
and
![]() becomes
becomes
![]() .
.