Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Above, we found that, for any integer
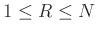 which divides
which divides
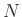 , a sufficient condition for perfect reconstruction is
, a sufficient condition for perfect reconstruction is
and the output signal is then
More generally, we allow any nonzero scaling and any additional delay:
where 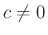 is any constant and
is any constant and 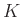 is any nonnegative integer.
In this case, the output signal is
is any nonnegative integer.
In this case, the output signal is
Thus, given any polyphase matrix
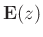 , we can attempt to
compute
, we can attempt to
compute
 :
:
- If it is stable, we can use it to build a
perfect-reconstruction filter bank.
- However, if
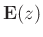 is FIR,
is FIR,
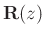 will typically be IIR.
will typically be IIR.
- In the next section, we will look at paraunitary filter banks,
for which
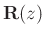 is FIR and paraunitary whenever
is FIR and paraunitary whenever
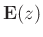 is.
is.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download JFB.pdf
Download JFB_2up.pdf
Download JFB_4up.pdf
[Comment on this page via email]
![]() which divides
which divides
![]() , a sufficient condition for perfect reconstruction is
, a sufficient condition for perfect reconstruction is
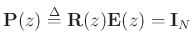
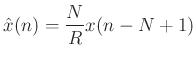
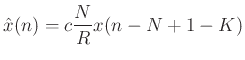
![]() , we can attempt to
compute
, we can attempt to
compute
![]() :
: