Polyphase View of the STFT

As a familiar special case, set

$$\bold{E}(z) = \bold{W}_N^\ast$$

where $\bold{W}_N^\ast$ is the DFT matrix:

$$\bold{W}_N^\ast[kn] = \left[e^{-j2\pi kn/N}\right].$$

The inverse of this polyphase matrix is then simply the inverse DFT matrix:

$$\bold{R}(z) = \frac{1}{N}\bold{W}_N$$

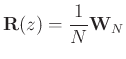
We see that the STFT can be seen as the simple special case of a perfect reconstruction filter bank for which the polyphase matrix is constant. It is also unitary when $\bold{E}(z)=\bold{W}_N^\ast/\sqrt{N}$ and $\bold{R}(z)=\bold{W}_N/\sqrt{N}$ .

The channel analysis and synthesis filters are, respectively,

$$\begin{eqnarray*} H_k(z) &=& H_0(zW_N^k)\\ [0.1in] F_k(z) &=& F_0(zW_N^{-k}) \end{eqnarray*}$$

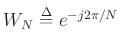where $W_N\mathrel{\stackrel{\mathrm{\Delta}}{=}}e^{-j2\pi/N}$ , as usual, and

$$F_0(z)=H_0(z)=\sum_{n=0}^{N-1}z^{-n}\leftrightarrow[1,1,\ldots,1]$$

corresponding to the rectangular window.

Looking again at the polyphase representation of the $N$ -channel filter bank with hop size $R$ , $\bold{E}(z)=\bold{W}_N^\ast$ , $\bold{R}(z)=\bold{W}_N$ , $R$ dividing $N$ , we have

Thus,

$$\zbox{\hbox{The polyphase representation is an \emph{overlap-add} representation}}$$

• Our analysis showed that the STFT using a rectangular window is a perfect reconstruction filter bank for all integer hop sizes in the set $R\in\{N,N/2,N/3,\ldots,N/N\}$ .
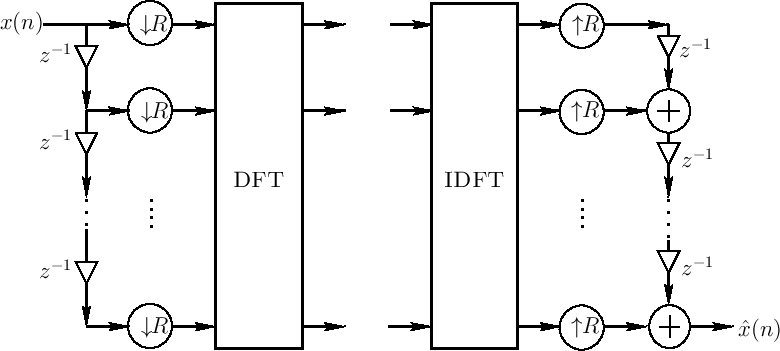
• The same type of analysis can be applied to the STFT using the other windows we've studied, including Portnoff windows.