Conjugate Quadrature Filters (CQF)

A class of causal, FIR, two-channel, criticially sampled, exact perfect-reconstruction filter-banks is the set of so-called Conjugate Quadrature Filters (CQF).

In the z-domain, the CQF relationships are

$$H_1(z) = z^{-(L-1)}H_0(-z^{-1})$$

In the time domain, the analysis and synthesis filters are given by

$$\begin{eqnarray*} h_1[n] &=& -(-1)^n h_0[L-1-n] \\ [0.1in] f_0[n] &=& h_0[L-1-n] \\ [0.1in] f_1[n] &=& -(-1)^n h_0(n) = - h_1(L-1-n) \end{eqnarray*}$$

That is, $f_0=\hbox{\sc Flip}(h_0)$ for the lowpass channel, and the highpass channel filters are a modulation of their lowpass counterparts by $(-1)^n$ .

• Again, all four analysis and synthesis filters are determined by the lowpass analysis filter $H_0(z)$ .

• It can be shown that this is an orthogonal filter bank.

• The analysis filters $H_0(z)$ and $H_1(z)$ are power complementary, i.e.,
  $$\left\vert H_0{e^{j\omega}}\right\vert^2 + \left\vert H_1{e^{j\omega}}\right\vert^2 = 1 \qquad\hbox{(Power Complementary)}$$
  or
  $${\tilde H}_0(z) H_0(z) + {\tilde H}_1(z) H_1(z) = 1 \qquad\hbox{(Power Complementary)}$$
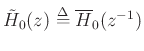  where ${\tilde H}_0(z)\mathrel{\stackrel{\mathrm{\Delta}}{=}}\overline{H}_0(z^{-1})$ denotes the paraconjugate of $H_0(z)$ (for real filters $H_0$ ). The paraconjugate is the analytic continuation of $\overline{H_0(e^{j\omega})}$ from the unit circle to the $z$ plane.

• Moreover, the analysis filters $H_0(z)$ are power symmetric, e.g.,
  $${\tilde H}_0(z) H_0(z) + {\tilde H}_0(-z) H_0(-z) \qquad\hbox{(Power Symmetric)}$$

• The power symmetric case was introduced by Smith and Barnwell in 1984.

With the CQF constraints, () reduces to

$$\hat{X}(z) = \frac{1}{2}[H_0(z)H_0(z^{-1}) + H_0(-z)H_0(-z^{-1})]X(z) \protect$$ (7)

Let $P(z) = H_0(z)H_0(-z)$ , such that $H_0(z)$ is a spectral factor of the half-band filter $P(z)$ (i.e., $P(e^{j\omega})$ is a nonnegative power response which is lowpass, cutting off near $\omega=\pi/4$ ). Then, () reduces to

$$\hat{X}(z) = \frac{1}{2}[P(z) + P(-z)]X(z) = -z^{-(L-1)}X(z)$$ (8)

• The problem of the PR filter design has been reduced to designing one half-band filter, $P(z)$ .
• It can be shown that any half-band filter can be written in the form $p[2n] = \delta[n]$ . That is, all non-zero even-idexed values of $p[n]$ are set to zero.

A simple design of an FIR half-band filter would be to window a sinc function:

$$p[n] = \frac{\hbox{sin}[\pi n/2]}{\pi n/2}w[n]$$ (9)

where $w[n]$ is any suitable window, such as the Kaiser window.

• Note that as a result of (), the CQF filters are power complementary. That is, they satisfy:
  $$\left\vert H_0(e^{j \omega})\right\vert^2 + \left\vert H_1(e^{j \omega})\right\vert^2 = 2$$

• Also note that the filters $H_0$ and $H_1$ are not linear phase.

• It can be shown that there are no two-channel perfect reconstruction filter banks that have all three of the following characteristics (except for the Haar filters):
  • FIR
  • orthogonality
  • linear phase

  In this design procedure, we have chosen to satisfy the first two and give up the third.

• By relaxing ``orthogonality'' to ``biorthogonality'', it becomes possible to obtain FIR linear phase filters in a critically sampled, perfect reconstruction filter bank. (See later section on Wavelet filter banks.)