Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Let's begin with a simple two-channel case, with lowpass analysis
filter 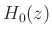 , highpass analysis filter
, highpass analysis filter 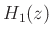 , lowpass synthesis
filter
, lowpass synthesis
filter 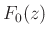 , and highpass synthesis filter
, and highpass synthesis filter  :
:
The outputs of the two analysis filters are then
After downsampling, the signals become
After upsampling, the signals become
After substitutions and rearranging, the output 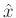 is a
filtered replica plus an aliasing term:
is a
filtered replica plus an aliasing term:
We require the second term (the aliasing term) to be zero for
perfect reconstruction.
This is arranged if we set
Thus,
- The synthesis lowpass filter
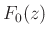 is the rotation by
is the rotation by 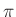 of the analysis highpass filter
of the analysis highpass filter 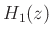 on the unit circle. If
on the unit circle. If
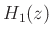 is highpass, cutting off at
is highpass, cutting off at
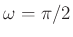 , then
, then 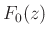 will be lowpass, cutting off at
will be lowpass, cutting off at 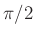 .
.
- The synthesis
highpass filter
 is the negative of the
is the negative of the 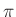 -rotation of the
analysis lowpass filter
-rotation of the
analysis lowpass filter 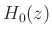 .
.
Note that aliasing is completely canceled by this choice of synthesis
filters  , for any choice of analysis filters
, for any choice of analysis filters  .
.
For perfect reconstruction, we additionally need
where
 is any constant
is any constant  times a linear-phase
term corresponding to
times a linear-phase
term corresponding to  samples of delay.
samples of delay.
Choosing  and
and 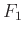 to cancel aliasing,
to cancel aliasing,
Perfect reconstruction thus also imposes a constraint on the analysis
filters, which is of course true for any band-splitting filter bank.
Let
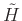 denote
denote  . Then both constraints can be expressed in
matrix form as
. Then both constraints can be expressed in
matrix form as
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download JFB.pdf
Download JFB_2up.pdf
Download JFB_4up.pdf
[Comment on this page via email]
![]() , highpass analysis filter
, highpass analysis filter ![]() , lowpass synthesis
filter
, lowpass synthesis
filter ![]() , and highpass synthesis filter
, and highpass synthesis filter ![]() :
:

![$\displaystyle V_k(z) = \frac{1}{2}\left[X_k(z^{1/2}) + X_k(-z^{1/2})\right], \; k=0,1
$](img112.png)
![$\displaystyle \frac{1}{2}[X_k(z) + X_k(-z)]$](img115.png)
![$\displaystyle \frac{1}{2}[H_k(z)X(z) + H_k(-z)X(-z)],\; k=0,1$](img116.png)
![]() and
and ![]() to cancel aliasing,
to cancel aliasing,
![]() denote
denote ![]() . Then both constraints can be expressed in
matrix form as
. Then both constraints can be expressed in
matrix form as
![$\displaystyle \left[\begin{array}{cc} H_0 & H_1 \\ [2pt] {\tilde H}_0 & {\tilde H}_1 \end{array}\right]\left[\begin{array}{c} F_0 \\ [2pt] F_1 \end{array}\right]=\left[\begin{array}{c} c \\ [2pt] 0 \end{array}\right]
$](img145.png)