Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Linear Phase Terms
The reason
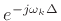 is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency:
Thus, the slope of the phase, viewed as a linear function of
radian-frequency 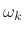 , is
, is 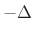 . In general, the time
delay in samples equals minus the slope of the linear phase
term. If we express the original spectrum in polar form as
. In general, the time
delay in samples equals minus the slope of the linear phase
term. If we express the original spectrum in polar form as
where 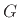 and
and 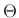 are the magnitude and phase of
are the magnitude and phase of 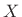 , respectively
(both real), we can see that a linear phase term only modifies the spectral
phase
, respectively
(both real), we can see that a linear phase term only modifies the spectral
phase 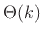 :
:
where
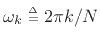 . A positive time delay (waveform shift to
the right) adds a negatively sloped linear phase to the original
spectral phase. A negative time delay (waveform shift to the left) adds a
positively sloped linear phase to the original spectral phase. If we
seem to be belaboring this relationship, it is because it is one of the
most useful in practice.
. A positive time delay (waveform shift to
the right) adds a negatively sloped linear phase to the original
spectral phase. A negative time delay (waveform shift to the left) adds a
positively sloped linear phase to the original spectral phase. If we
seem to be belaboring this relationship, it is because it is one of the
most useful in practice.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency:
![$\displaystyle e^{-j \omega_k \Delta} X(k) \isdef
e^{-j \omega_k \Delta} G(k) e^{j\Theta(k)}
= G(k) e^{j[\Theta(k)-\omega_k\Delta]}
$](img1369.png)