Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In practice, a signal may be said to be linear phase
when its phase is of the form
where  is any real constant (usually an integer), and
is any real constant (usually an integer), and
 is an indicator function which takes on the
values 0
or
is an indicator function which takes on the
values 0
or 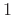 over the points
over the points 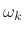 ,
,
 .
An important class of examples is when the signal is regarded as a
filter impulse response.7.15 What all such
signals have in common is that they are
symmetric about the time
.
An important class of examples is when the signal is regarded as a
filter impulse response.7.15 What all such
signals have in common is that they are
symmetric about the time 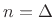 in the time domain
(as we will show on the next page). Thus, the term ``linear phase
signal'' often really means ``a signal whose phase is linear between
in the time domain
(as we will show on the next page). Thus, the term ``linear phase
signal'' often really means ``a signal whose phase is linear between
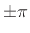 discontinuities.''
discontinuities.''
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]