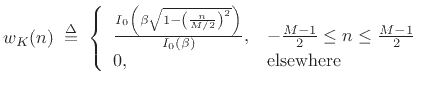 |
(4.39) |
Jim Kaiser discovered a simple approximation to the DPSS window based upon Bessel functions [115], generally known as the Kaiser window (or Kaiser-Bessel window).
Definition:
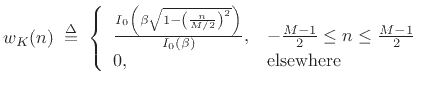 |
(4.39) |
Window transform:
The Fourier transform of the Kaiser window ![]() (where
(where ![]() is
treated as continuous) is given by4.11
is
treated as continuous) is given by4.11
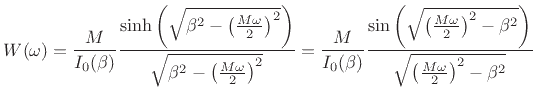 |
(4.40) |
![$\displaystyle I_0(x) \isdefs \sum_{k=0}^{\infty} \left[ \frac{\left(\frac{x}{2}\right)^k}{k!} \right]^2
$](img486.png)
Notes:
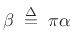 |
(4.42) |