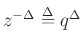Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Lagrange interpolation is just polynomial interpolation
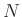 th-order polynomial interpolates
th-order polynomial interpolates 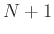 points
points
- First-order case = linear interpolation
Problem Formulation
Given a set of 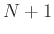 known samples
known samples  ,
,
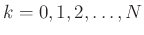 , find the
unique order
, find the
unique order 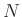 polynomial
polynomial 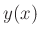 which interpolates the samples
which interpolates the samples
Solution (Waring, Lagrange):
where  is the Lagrange polynomial corresponding to sample
is the Lagrange polynomial corresponding to sample 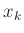 :
:
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Interpolation.pdf
Download Interpolation_2up.pdf
Download Interpolation_4up.pdf
Visit the online book containing this material.
![]() known samples
known samples ![]() ,
,
![]() , find the
unique order
, find the
unique order ![]() polynomial
polynomial ![]() which interpolates the samples
which interpolates the samples
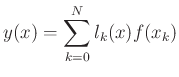
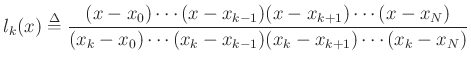
![$\displaystyle l_k(x_j) = \delta_{kj} \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\{\begin{array}{ll}
1, & j=k \\ [5pt]
0, & j\neq k \\
\end{array} \right.
$](img93.png)