Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Chebyshev Polynomials
Figure 3.34:
![\includegraphics[width=\twidth]{eps/first-even-chebs-c}](img530.png) |
The 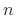 th Chebyshev polynomial may be defined by
th Chebyshev polynomial may be defined by
![$\displaystyle T_n(x) = \left\{\begin{array}{ll} \cos[n\cos^{-1}(x)], & \vert x\vert\le1 \\ [5pt] \cosh[n\cosh^{-1}(x)], & \vert x\vert>1 \\ \end{array} \right..$](img531.png) |
(4.46) |
The first three even-order cases are plotted in
Fig.3.35. (We will only need the even orders for
making Chebyshev windows, as only they are symmetric about time 0.)
Clearly, 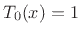 and
and 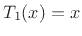 . Using the double-angle trig
formula
. Using the double-angle trig
formula
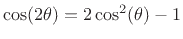 , it can be verified that
, it can be verified that
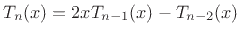 |
(4.47) |
for 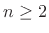 .
The following properties of the Chebyshev polynomials are well known:
.
The following properties of the Chebyshev polynomials are well known:
 is an
is an 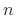 th-order polynomial in
th-order polynomial in 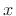 .
.
 is an even function when
is an even function when 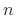 is an even integer,
and odd when
is an even integer,
and odd when 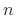 is odd.
is odd.
 has
has 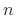 zeros in the open interval
zeros in the open interval  , and
, and
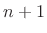 extrema in the closed interval
extrema in the closed interval ![$ [-1,1]$](img540.png) .
.
 for
for  .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=\twidth]{eps/first-even-chebs-c}](img530.png)
![]() th Chebyshev polynomial may be defined by
th Chebyshev polynomial may be defined by
![$\displaystyle T_n(x) = \left\{\begin{array}{ll} \cos[n\cos^{-1}(x)], & \vert x\vert\le1 \\ [5pt] \cosh[n\cosh^{-1}(x)], & \vert x\vert>1 \\ \end{array} \right..$](img531.png)