Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let  denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
![$\displaystyle W(\omega) = \frac{T_{M-1}[x_0 \cos(\omega/2)]}{T_{M-1}(x_0)}$](img543.png) |
(4.48) |
where 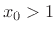 is defined by the desired ripple specification:
is defined by the desired ripple specification:
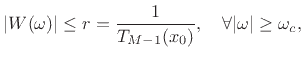 |
(4.49) |
where 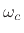 is the ``main lobe edge frequency'' defined by
is the ``main lobe edge frequency'' defined by
![$\displaystyle \omega_c \isdefs 2\cos^{-1}\left[\frac{1}{x_0}\right].$](img546.png) |
(4.50) |
Expanding the trigonometric polynomial 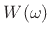 in terms of complex exponentials yields
in terms of complex exponentials yields
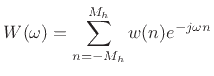 |
(4.51) |
where
 . Thus, the coefficients
. Thus, the coefficients 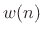 give the
length
give the
length  Dolph-Chebyshev window in zero-phase form.
Dolph-Chebyshev window in zero-phase form.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
![$\displaystyle W(\omega) = \frac{T_{M-1}[x_0 \cos(\omega/2)]}{T_{M-1}(x_0)}$](img543.png)
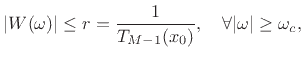
![$\displaystyle \omega_c \isdefs 2\cos^{-1}\left[\frac{1}{x_0}\right].$](img546.png)
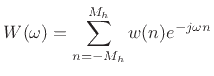
 . Thus, the coefficients
. Thus, the coefficients