Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Define the backwards difference operator 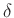 by
by
and the factorial polynomials (aka rising factorials or
Pochhammer symbol) by
These give a discrete-time counterpart to
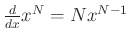 , viz.,
, viz.,
In these terms, a discrete-time Taylor series about  can be defined:
can be defined:
- Known as ``Newton's Backward Difference Formula''
- Truncating this expansion at
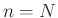 again yields
again yields 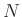 th-order
Lagrange interpolation on uniformly spaced samples
th-order
Lagrange interpolation on uniformly spaced samples
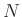 th-order Lagrange interpolation via truncated discrete-time
Taylor series expansion about time
th-order Lagrange interpolation via truncated discrete-time
Taylor series expansion about time  :
:
Each term in the expansion can be computed recursively from the previous term:
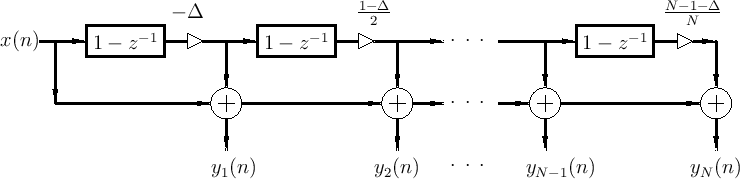
This gives the same efficient computational form found previously:
where
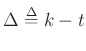 is the desired delay for
fractional-delay filtering, and
is the desired delay for
fractional-delay filtering, and 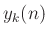 is the output signal for
is the output signal for
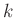 th-order Lagrange interpolation (modular!). See also
Newton's divided difference interpolation formula.
th-order Lagrange interpolation (modular!). See also
Newton's divided difference interpolation formula.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Interpolation.pdf
Download Interpolation_2up.pdf
Download Interpolation_4up.pdf
Visit the online book containing this material.
![]() by
by
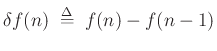
![$\displaystyle x^{[N]} \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;x(x+1)(x+2)\cdots(x + N - 2) (x + N - 1)
$](img172.png)
![$\displaystyle \hat{f}(t) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;\sum_{n=0}^\infty [\delta^n f(k)]\frac{(t-k)^{[n]}}{n!}
$](img176.png)
![]() th-order Lagrange interpolation via truncated discrete-time
Taylor series expansion about time
th-order Lagrange interpolation via truncated discrete-time
Taylor series expansion about time ![]() :
:
![$\displaystyle \hat{f}(t) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;\sum_{n=0}^N [\delta^n f(k)]\frac{(t-k)^{[n]}}{n!}
$](img178.png)
![\begin{eqnarray*}[\delta^n f(k)]\frac{(t-k)^{[n]}}{n!} &=& [\delta^{n-1} f(k)]\frac{(t-k)^{[n-1]}}{(n-1)!} \; \times\\
& & \zbox{\frac{t-k+N-1}{N}\cdot[\delta f(k)]}
\end{eqnarray*}](img179.png)
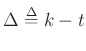 is the desired delay for
fractional-delay filtering, and
is the desired delay for
fractional-delay filtering, and