Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Basic idea: Each FIR filter coefficient 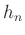 becomes an order
becomes an order
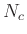 polynomial in the delay parameter
polynomial in the delay parameter 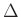 :
:
- More generally:
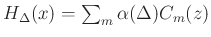
where
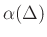 is provided by a table lookup
is provided by a table lookup
- Basic idea applies to any one-parameter filter variation
- Also applies to time-varying filters
(
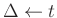 )
)
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Interpolation.pdf
Download Interpolation_2up.pdf
Download Interpolation_4up.pdf
Visit the online book containing this material.
![]() becomes an order
becomes an order
![]() polynomial in the delay parameter
polynomial in the delay parameter ![]() :
:
![\begin{eqnarray*}
h_\Delta(n) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \sum_{m=0}^{N_c}c_n(m)\Delta^m, \quad n=0,1,2,\ldots,{N_h}\\
\Leftrightarrow \;
H_\Delta(z) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \sum_{n=0}^{N_h}h_\Delta(n)z^{-n} \\
&=& \sum_{n=0}^{N_h}\left[\sum_{m=0}^{N_c}c_n(m)\Delta^m\right]z^{-n}\\
&=& \sum_{m=0}^{N_c}\left[\sum_{n=0}^{N_h}c_n(m) z^{-n}\right]\Delta^m \\
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \sum_{m=0}^{N_c}C_m(z) \Delta^m
\end{eqnarray*}](img123.png)