Taylor Series Expansion of $z^{-\Delta} \mathrel{\stackrel{\mathrm{\Delta}}{=}}q^\Delta$

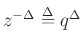
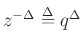
To obtain a causal FIR filter, we will expand $H_\Delta(z)$ in powers of $z^{-1}$ instead of $z$ . For simplicity of notation, define $q=z^{-1}$ . Then we obtain the Taylor series expansion of $H_\Delta(q^{-1}) = q^\Delta$ about $q=1$ to be

$$\begin{eqnarray*} H_\Delta(q^{-1}) &=& H_\Delta(1) + H'_\Delta(1)(q-1) + \frac{1}{2}H''_\Delta(1)(q-1)^2 + \frac{1}{3!}H'''_\Delta(1)(q-1)^3 + \cdots\\ &=& 1 + \left.\Delta\,q^{\Delta-1}\right\vert _{q=1} (q-1) + \frac{1}{2}\Delta(\Delta-1)\left.q^{\Delta-2}\right\vert _{q=1}(q-1)^2 + \cdots\\ &=& 1 + \Delta\cdot(q-1) + \frac{1}{2}\Delta(\Delta-1)\cdot (q-1)^2 + \frac{1}{3!}\Delta(\Delta-1)(\Delta-2)\cdot (q-1)^3 + \cdots\\ \end{eqnarray*}$$

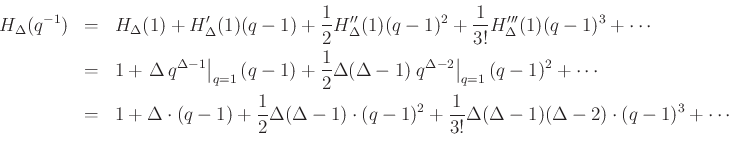
where the derivatives are with respect to $q=z^{-1}$ , e.g., $H'_\Delta(q) \mathrel{\stackrel{\scriptscriptstyle\mathrm{\Delta}}{\scriptstyle=}}\frac{d}{dq}q^\Delta=\Delta q^{\Delta-1}$ . Our maximally flat $N$ th-order Langrange FIR interpolation filter is obtain by truncating this expansion at order $N$ :

$$\begin{eqnarray*} \hat{H}_\Delta(q^{-1}) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& 1 + \Delta(q-1) + \frac{1}{2}\Delta(\Delta-1)(q-1)^2 + \frac{1}{3!}\Delta(\Delta-1)(\Delta-2)(q-1)^3 \\ && \quad + \cdots + \frac{1}{N!}\left[\prod_{k=0}^{N-1}(\Delta-k)\right]\, (q-1)^N\\ &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \hbar _\Delta(0) + \hbar _\Delta(1) (q-1) + \hbar _\Delta(2) (q-1)^2 + \cdots + \hbar _\Delta(N) (q-1)^N \end{eqnarray*}$$

where

$$\hbar _\Delta(n) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;\frac{1}{n!}\prod_{k=0}^{n-1}(\Delta-k) \;=\;\frac{\Delta(\Delta-1)(\Delta-2)\cdots(\Delta-n+1)}{n!}$$

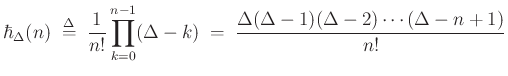
This can be viewed as an FIR filter structure in which the usual delay elements are replaced by $q-1 = z^{-1}-1$ .