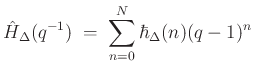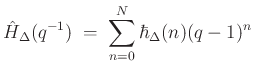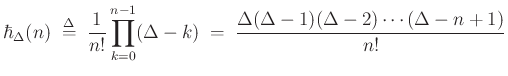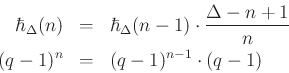Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Our Lagrange interpolation filter is again
where the coefficients of
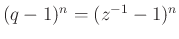 are again
are again
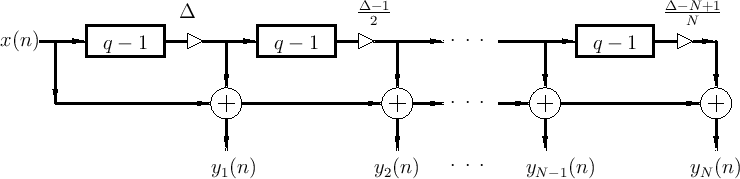
Note that we can recursively compute the terms in the sum from left to right:
Thus, we can crank out the terms in series and sum the intermediate signals:
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Interpolation.pdf
Download Interpolation_2up.pdf
Download Interpolation_4up.pdf
Visit the online book containing this material.