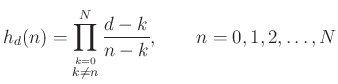Lagrange Interpolation in Faust, Variable Delay $d$

With variable delay, it is easiest to work with the plain FIR form, because the interpolation coefficients can jump around at will along the delay:

import("music.lib");

fdelayltv(N,n,d,x) = sum(i, N+1, delay(n,id+i,x) * h(N,fd,i))
with {
  o = (N-1.00001)/2;  // ~center FIR interpolator
  dmo = d - o; // assumed >=0 [d > (N-1)/2]
  id = int(dmo);
  fd = o + frac(dmo);
  h(N,d,n) = facs1(N,d,n) * facs2(N,d,n);
  facs1(N,d,n) = select2(n,1,prod(k,max(1,n),
                             select2(k<n,1,fac(d,n,k))));
  facs2(N,d,n) = select2(n<N,1,prod(l,max(1,N-n),
                             fac(d,n,l+n+1)));
  fac(d,n,k) = (d-k)/((n-k)+(n==k));
};

process = fdelayltv(5,1024,5.4); // 5th-order ex.

Recall explicit formula for Lagrange interpolation coefficients:

$$h_d(n) = \prod_{\stackrel{k=0}{k\neq n}}^N \frac{d-k}{n-k},\qquad n=0,1,2,\ldots,N$$