


Next: Boundary Conditions
Up: Elastic Solids
Previous: Phase and Group Velocities
Scattering Networks for the Navier System
Nitsche has represented this system as an MDKC in [131]. Choosing current-like variables
he derived an MDKC for the Navier system, which we have reproduced (with some minor changes) at top in Figure 5.25, where coordinates defined by the transformation matrix (3.24) have been used. Notice that again, because 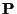 is not diagonal, the time derivatives of the components
is not diagonal, the time derivatives of the components
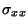 ,
,
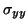 and
and
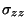 are coupled. In the circuit representation, this is represented by a three-port coupled inductance of the form of (2.48), with a matrix inductance
are coupled. In the circuit representation, this is represented by a three-port coupled inductance of the form of (2.48), with a matrix inductance
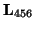 defined by
defined by
where the inductances 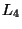 ,
, 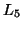 ,
, 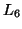 and
and
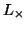 appear in the figure.
appear in the figure.
The positivity condition on the inductances 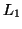 ,
, 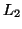 ,
, 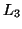 ,
, 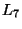 ,
, 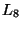 and
and 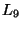 , as well as a positive definiteness condition on the matrix
, as well as a positive definiteness condition on the matrix
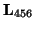 gives, as optimal choices of the parameters
gives, as optimal choices of the parameters 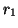 and
and 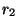 ,
,
and a bound on 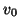 ,
,
When the material parameters are constant, 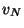 reduces to
reduces to
A modified MDKC is shown at top in Figure 5.26, where velocities are treated as currents, and stresses as voltages; as such, the coupled inductance in Figure 5.25 has become a coupled capacitance. This network may be discretized in a way very similar to the network for Maxwell's Equations, as described in §4.10.6. Under the spectral mappings defined by (4.112) (with step sizes of
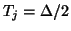 ,
,
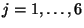 ), the connecting LSI two-ports decompose into series/parallel connections of multidimensional unit elements. The one-port inductances and capacitances, as well as the coupled capacitance are discretized using the trapezoid rule, with a step size of
), the connecting LSI two-ports decompose into series/parallel connections of multidimensional unit elements. The one-port inductances and capacitances, as well as the coupled capacitance are discretized using the trapezoid rule, with a step size of
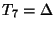 . The resulting multidimensional DWN is shown at bottom in Figure 5.26, and the interleaved computational grid in Figure 5.27 (which is very similar to the grid for the DWN for Maxwell's Equations, as shown in Figure 4.55).
. The resulting multidimensional DWN is shown at bottom in Figure 5.26, and the interleaved computational grid in Figure 5.27 (which is very similar to the grid for the DWN for Maxwell's Equations, as shown in Figure 4.55).



Next: Boundary Conditions
Up: Elastic Solids
Previous: Phase and Group Velocities
Stefan Bilbao
2002-01-22
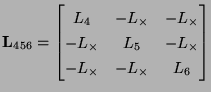
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() , as well as a positive definiteness condition on the matrix
, as well as a positive definiteness condition on the matrix
![]() gives, as optimal choices of the parameters
gives, as optimal choices of the parameters ![]() and
and ![]() ,
,
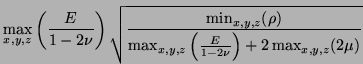
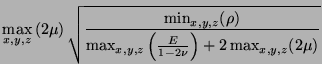
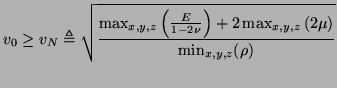
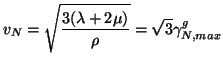
![]() ,
,
![]() ), the connecting LSI two-ports decompose into series/parallel connections of multidimensional unit elements. The one-port inductances and capacitances, as well as the coupled capacitance are discretized using the trapezoid rule, with a step size of
), the connecting LSI two-ports decompose into series/parallel connections of multidimensional unit elements. The one-port inductances and capacitances, as well as the coupled capacitance are discretized using the trapezoid rule, with a step size of
![]() . The resulting multidimensional DWN is shown at bottom in Figure 5.26, and the interleaved computational grid in Figure 5.27 (which is very similar to the grid for the DWN for Maxwell's Equations, as shown in Figure 4.55).
. The resulting multidimensional DWN is shown at bottom in Figure 5.26, and the interleaved computational grid in Figure 5.27 (which is very similar to the grid for the DWN for Maxwell's Equations, as shown in Figure 4.55).