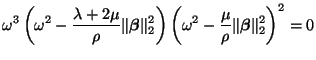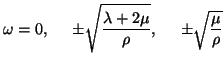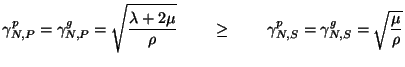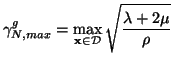Phase and Group Velocities

The characteristic polynomial relation for the Navier system, in terms of frequencies 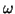$\omega$ and wavenumbers 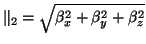$\Vert$$\beta$$\Vert _{2} = \sqrt{\beta_{x}^{2}+\beta_{y}^{2} + \beta_{z}^{2}}$, will be

$$\omega^{3}\left(\omega^{2}-\frac{\lambda+2\mu}{\rho}\Vert\mbox{\b... ...a^{2}-\frac{\mu}{\rho}\Vert\mbox{\boldmath$\beta$}\Vert _{2}^{2}\right)^{2} = 0$$

and has roots

$$\omega = 0, \hspace{0.2in}\pm\sqrt{\frac{\lambda+2\mu}{\rho}}, \hspace{0.2in}\pm\sqrt{\frac{\mu}{\rho}}$$

Ignoring the non-propagating modes with frequency 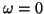$\omega = 0$, and the multiplicities of the other modes, we can see that wave propagation is dispersionless, at least for the constant-coefficient problem. There are two wave speeds,

$$\gamma_{N, P}^{p} =\gamma_{N, P}^{g} = \sqrt{\frac{\lambda+2\mu}{... ...eq\hspace{0.3in} \gamma_{N, S}^{p} =\gamma_{N, S}^{g} = \sqrt{\frac{\mu}{\rho}}$$

which are also known as the P-wave and S-wave (or compressional and shear wave) speeds [35].

For the varying-coefficient problem, the global maximum group velocity is then

$$\gamma_{N, max}^{g} = \max_{{\bf x}\in\mathcal{D}}\sqrt{\frac{\lambda+2\mu}{\rho}}$$