| (5.22) |
Consider again the Timoshenko system of (5.17) and (5.18). We can scale the variables just as for the transmission line (see §3.7). That is, we can write
|
|
|
|
The constant proportional terms on the right-hand side appear anti-symmetrically, and can be interpreted as a lossless gyrator coupling. We can now write down a MDKC for the scaled system of equations; it is shown, along with element values in Figure 5.5. Its MDWD counterpart is pictured in Figure 5.6. Here, we have used the coordinate transformation defined in (3.18) with step sizes
![]() . We have used
. We have used
![]() for the one-port time inductors.
for the one-port time inductors.
A comment is necessary regarding the gyrator in Figure 5.6. In order to deal with the delay-free loop which arises from the placement of a gyrator between two series junctions, we have set the corresponding ports of the series junctions on either side of the gyrator to be reflection-free. This, however, means that the two port resistances of the gyrator are not, in general, equal to the gyrator constant, which, in this case, will be ![]() . In terms of wave variables, the signal flow diagram of the gyrator will not be of the simple form of (2.26), but takes the more general form of (2.25) mentioned in §2.3.4. It is of course also possible to set only one of the ports connected to the gyrator to be reflection-free, (say
. In terms of wave variables, the signal flow diagram of the gyrator will not be of the simple form of (2.26), but takes the more general form of (2.25) mentioned in §2.3.4. It is of course also possible to set only one of the ports connected to the gyrator to be reflection-free, (say
![]() ), and then the other port resistance to be
), and then the other port resistance to be
![]() , in which case the general gyrator form degenerates to a pair of scalings.
, in which case the general gyrator form degenerates to a pair of scalings.
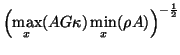 |
|||
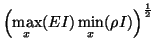 |