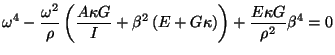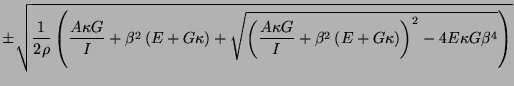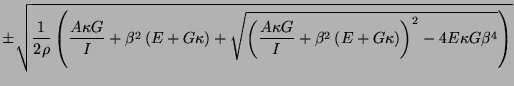Dispersion

The characteristic polynomial equation, from (3.10) with the system matrices given above, in the case of constant coefficients, is

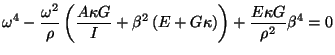$$\omega^{4}-\frac{\omega^{2}}{\rho}\left(\frac{A\kappa G}{ I} +\beta^{2}\left(E+G\kappa\right)\right)+\frac{E\kappa G}{\rho^{2}}\beta^{4} = 0$$ (5.20)

where 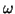$\omega$ and $\beta$ are frequency and spatial wavenumber, respectively. There are two pairs of solutions to this equation, which can be written as

$$\omega_{1\pm} = \pm\sqrt{\frac{1}{2\rho}\left(\frac{A\kappa G}{I} +\beta^{2}\left... ... G}{I} +\beta^{2}\left(E+G\kappa\right)\right)^{2}-4E\kappa G\beta^{4}}\right)}$$

$$\omega_{2\pm} = \pm\sqrt{\frac{1}{2\rho}\left(\frac{A\kappa G}{I} +\beta^{2}\left... ... G}{I} +\beta^{2}\left(E+G\kappa\right)\right)^{2}-4E\kappa G\beta^{4}}\right)}$$

and it is simple to show that in contrast with the Euler-Bernoulli beam, the group velocities will be bounded. Indeed, we have in particular that

$$\lim_{\beta\rightarrow\infty}\omega_{1\pm} = \pm\beta\frac{E}{\rh... ...e{0.5in} \lim_{\beta\rightarrow\infty}\omega_{2\pm}\pm\beta\frac{G\kappa}{\rho}$$

the first of these relations is similar to that which describes longitudinal wave propagation in a bar, and the second corresponds to shear vibration [77]. For the full varying-coefficient problem, the maximum group velocity, as defined in (3.13), will be

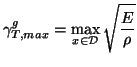$$\gamma_{T, max}^{g} = \max_{x\in\mathcal{D}}\sqrt{\frac{E}{\rho}}$$ (5.21)