Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The window method for digital filter design is fast,
convenient, and robust, but generally suboptimal. It is easily
understood in terms of the convolution theorem for Fourier
transforms, making it instructive to study after the Fourier theorems
and windows for spectrum analysis. It can be effectively combined
with the frequency sampling method, as we will see in §4.6
below.
The window method consists of simply ``windowing'' a theoretically
ideal filter impulse response 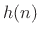 by some suitably chosen window
function
by some suitably chosen window
function 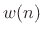 , yielding
, yielding
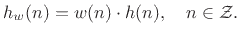 |
(5.8) |
For example, as derived in Eq.(4.3), the impulse response of the
ideal lowpass filter is the well known sinc function
where  is the total normalized bandwidth of the lowpass filter
in Hz (counting both negative and positive frequencies), and
is the total normalized bandwidth of the lowpass filter
in Hz (counting both negative and positive frequencies), and 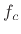 denotes the cut-off frequency in Hz. As noted earlier, we cannot
implement this filter in practice because it is noncausal and
infinitely long.
denotes the cut-off frequency in Hz. As noted earlier, we cannot
implement this filter in practice because it is noncausal and
infinitely long.
Since
 sinc
sinc decays away from time 0 as
decays away from time 0 as  , we would
expect to be able to truncate it to the interval
, we would
expect to be able to truncate it to the interval ![$ [-N,N]$](img702.png) , for some
sufficiently large
, for some
sufficiently large  , and obtain a pretty good FIR filter which
approximates the ideal filter. This would be an example of using the
window method with the rectangular window. We saw in
§4.3 that such a choice is optimal in the least-squares
sense, but it designs relatively poor audio filters. Choosing other
windows corresponds to tapering the ideal impulse response to
zero instead of truncating it. Tapering better preserves the shape of
the desired frequency response, as we will see. By choosing the
window carefully, we can manage various trade-offs so as to maximize
the filter-design quality in a given application.
, and obtain a pretty good FIR filter which
approximates the ideal filter. This would be an example of using the
window method with the rectangular window. We saw in
§4.3 that such a choice is optimal in the least-squares
sense, but it designs relatively poor audio filters. Choosing other
windows corresponds to tapering the ideal impulse response to
zero instead of truncating it. Tapering better preserves the shape of
the desired frequency response, as we will see. By choosing the
window carefully, we can manage various trade-offs so as to maximize
the filter-design quality in a given application.
Window functions are always time limited. This means there is
always a finite integer  such that
such that 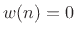 for all
for all
 . The final windowed impulse response
. The final windowed impulse response
 is thus always time-limited, as needed for practical
implementation. The window method always designs a
finite-impulse-response (FIR) digital filter (as opposed to an
infinite-impulse-response (IIR) digital filter).
is thus always time-limited, as needed for practical
implementation. The window method always designs a
finite-impulse-response (FIR) digital filter (as opposed to an
infinite-impulse-response (IIR) digital filter).
By the dual of the convolution theorem, pointwise multiplication in
the time domain corresponds to convolution in the frequency domain.
Thus, the designed filter  has a frequency response given by
has a frequency response given by
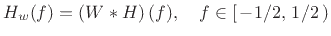 |
(5.10) |
where
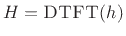 is the ideal frequency response and
is the ideal frequency response and
 is
the window transform. For the ideal lowpass filter,
is
the window transform. For the ideal lowpass filter,  is a
rectangular window in the frequency domain. The frequency response
is a
rectangular window in the frequency domain. The frequency response
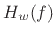 is thus obtained by convolving the rectangular window with
the window transform
is thus obtained by convolving the rectangular window with
the window transform 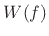 . This implies several points which can be
immediately seen in terms of this convolution operation:
. This implies several points which can be
immediately seen in terms of this convolution operation:
- The pass-band gain is primarily the area under the
main lobe of the window transform, provided the main lobe
``fits'' inside the pass-band (i.e., the total lowpass bandwidth
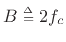 is greater than or equal to the main-lobe width
of
is greater than or equal to the main-lobe width
of 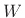 ).
).
- The stop-band gain is given by an integral over a portion
of the side lobes of the window transform. Since side-lobes
oscillate about zero, a finite integral over them is normally much
smaller than the side-lobes themselves, due to adjacent side-lobe
cancellation under the integral.
- The best stop-band performance occurs when the cut-off
frequency is set so that the stop-band side-lobe integral traverses a
whole number of side lobes.
- The transition bandwidth is equal to the bandwidth of
the main lobe of the window transform, again provided that the main
lobe ``fits'' inside the pass-band.
- For very small lowpass bandwidths
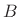 ,
, 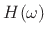 approaches an
impulse in the frequency domain. Since the impulse is the
identity operator under convolution, the resulting lowpass filter
approaches an
impulse in the frequency domain. Since the impulse is the
identity operator under convolution, the resulting lowpass filter
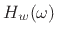 approaches the window transform
approaches the window transform 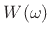 for small
for small
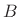 . In particular, the stop-band gain approaches the window
side-lobe level, and the transition width approaches half the
main-lobe width. Thus, for good results, the lowpass cut-off
frequency should be set no lower than half the window's main-lobe
width.
. In particular, the stop-band gain approaches the window
side-lobe level, and the transition width approaches half the
main-lobe width. Thus, for good results, the lowpass cut-off
frequency should be set no lower than half the window's main-lobe
width.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by some suitably chosen window
function
by some suitably chosen window
function ![]() , yielding
, yielding
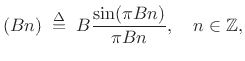
![]() sinc
sinc![]() decays away from time 0 as
decays away from time 0 as ![]() , we would
expect to be able to truncate it to the interval
, we would
expect to be able to truncate it to the interval ![]() , for some
sufficiently large
, for some
sufficiently large ![]() , and obtain a pretty good FIR filter which
approximates the ideal filter. This would be an example of using the
window method with the rectangular window. We saw in
§4.3 that such a choice is optimal in the least-squares
sense, but it designs relatively poor audio filters. Choosing other
windows corresponds to tapering the ideal impulse response to
zero instead of truncating it. Tapering better preserves the shape of
the desired frequency response, as we will see. By choosing the
window carefully, we can manage various trade-offs so as to maximize
the filter-design quality in a given application.
, and obtain a pretty good FIR filter which
approximates the ideal filter. This would be an example of using the
window method with the rectangular window. We saw in
§4.3 that such a choice is optimal in the least-squares
sense, but it designs relatively poor audio filters. Choosing other
windows corresponds to tapering the ideal impulse response to
zero instead of truncating it. Tapering better preserves the shape of
the desired frequency response, as we will see. By choosing the
window carefully, we can manage various trade-offs so as to maximize
the filter-design quality in a given application.
![]() such that
such that ![]() for all
for all
![]() . The final windowed impulse response
. The final windowed impulse response
![]() is thus always time-limited, as needed for practical
implementation. The window method always designs a
finite-impulse-response (FIR) digital filter (as opposed to an
infinite-impulse-response (IIR) digital filter).
is thus always time-limited, as needed for practical
implementation. The window method always designs a
finite-impulse-response (FIR) digital filter (as opposed to an
infinite-impulse-response (IIR) digital filter).
![]() has a frequency response given by
has a frequency response given by