FIR filters are basic in spectral audio signal processing. In fact,
the fastest way to implement long FIR filters in conventional
CPUs5.1 is by means of
FFT convolution.
The
convolution theorem for Fourier transforms (§2.3.5)
states that the convolution of an input signal ![]() with a filter
impulse-response
with a filter
impulse-response ![]() is given by the inverse DTFT of the product of
the signal's spectrum
is given by the inverse DTFT of the product of
the signal's spectrum ![]() times the filter's frequency
response
times the filter's frequency
response ![]() , i.e.,
, i.e.,
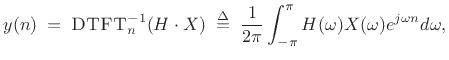 |
(5.1) |

and the DTFT is defined as (§2.1)
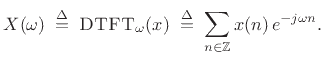 |
(5.2) |
This chapter provides a starting point in the area of FIR digital filter design. The so-called ``window method'' for FIR filter design, also based on the convolution theorem for Fourier transforms, is discussed in some detail, and compared with an optimal Chebyshev method. Other methods, such as least-squares, are discussed briefly to provide further perspective. Tools for FIR filter design in both Octave and the Matlab Signal Processing Toolbox are listed where applicable. For more information on digital filter design, see, e.g., the documentation for the Matlab Signal Processing Toolbox and/or [263,283,32,204,275,224,198,258].