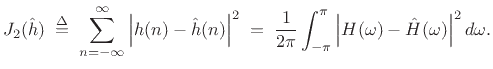Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Perhaps the most commonly employed error criterion in signal
processing is the least-squares error criterion.
Let 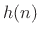 denote some ideal filter impulse response, possibly
infinitely long, and let
denote some ideal filter impulse response, possibly
infinitely long, and let
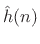 denote the impulse response of a
length
denote the impulse response of a
length  causal FIR filter that we wish to design. The sum of
squared errors is given by
causal FIR filter that we wish to design. The sum of
squared errors is given by
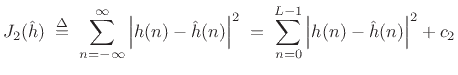 |
(5.4) |
where 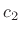 does not depend on
does not depend on 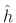 . Note that
. Note that
 .
We can minimize the error by simply matching the first
.
We can minimize the error by simply matching the first  terms in
the desired impulse response. That is, the optimal least-squares FIR
filter has the following ``tap'' coefficients:
terms in
the desired impulse response. That is, the optimal least-squares FIR
filter has the following ``tap'' coefficients:
![$\displaystyle {\hat h}(n) \isdef \left\{\begin{array}{ll} h(n), & 0\leq n \leq L-1 \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right. \protect$](img678.png) |
(5.5) |
The same solution works also for any
 norm (§4.10.1).
That is, the error
norm (§4.10.1).
That is, the error
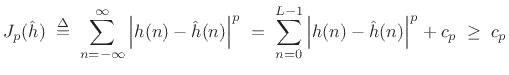 |
(5.6) |
is also minimized by matching the leading  terms of the desired
impulse response.
terms of the desired
impulse response.
In the
 (least-squares) case, we have, by the Fourier energy
theorem (§2.3.8),
(least-squares) case, we have, by the Fourier energy
theorem (§2.3.8),
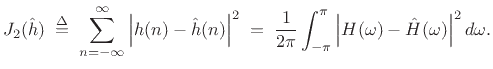 |
(5.7) |
Therefore,
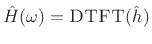 is an optimal least-squares
approximation to
is an optimal least-squares
approximation to 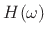 when
when 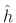 is given by (4.5). In
other words, the frequency response of the filter
is given by (4.5). In
other words, the frequency response of the filter 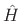 is optimal in
the
is optimal in
the
 (least-squares) sense.
(least-squares) sense.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote some ideal filter impulse response, possibly
infinitely long, and let
denote some ideal filter impulse response, possibly
infinitely long, and let
![]() denote the impulse response of a
length
denote the impulse response of a
length ![]() causal FIR filter that we wish to design. The sum of
squared errors is given by
causal FIR filter that we wish to design. The sum of
squared errors is given by
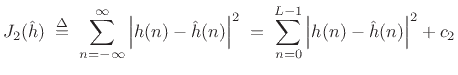
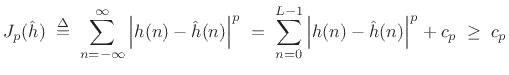
![]() (least-squares) case, we have, by the Fourier energy
theorem (§2.3.8),
(least-squares) case, we have, by the Fourier energy
theorem (§2.3.8),