The convolution of two signals ![]() and
and ![]() in
in
![]() may be
denoted ``
may be
denoted ``
![]() '' and defined by
'' and defined by

Note that this is circular convolution (or ``cyclic'' convolution).7.4 The importance of convolution in linear systems theory is discussed in §8.3.
Cyclic convolution can be expressed in terms of previously defined operators as
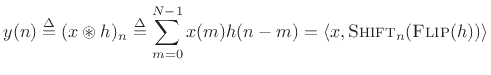
where