Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 8.1 illustrates the conceptual operation of filtering an input
signal 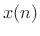 by a filter with impulse-response
by a filter with impulse-response 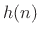 to produce an
output signal
to produce an
output signal 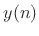 . By the convolution theorem for DTFTs
(§2.3.5),
. By the convolution theorem for DTFTs
(§2.3.5),
 |
(9.9) |
or,
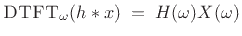 |
(9.10) |
where  and
and 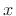 are arbitrary real or complex sequences, and
are arbitrary real or complex sequences, and  and
and
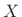 are the DTFTs of
are the DTFTs of  and
and 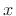 , respectively. The convolution
of
, respectively. The convolution
of 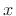 and
and  is defined by
is defined by
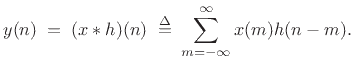 |
(9.11) |
In practice, we always use the DFT (preferably an FFT) in place of the
DTFT, in which case we may write
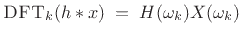 |
(9.12) |
where now
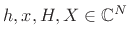 (length
(length 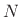 complex sequences). It is
important to remember that the specific form of convolution implied in
the DFT case is cyclic (also called
circular) convolution [264]:
complex sequences). It is
important to remember that the specific form of convolution implied in
the DFT case is cyclic (also called
circular) convolution [264]:
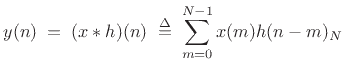 |
(9.13) |
where  means ``
means ``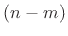 modulo
modulo 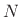 .''
.''
Another way to look at convolution is as the inner product of 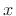 , and
, and
![$ \hbox{\sc Shift}_n[\hbox{\sc Flip}(h)]$](img1317.png) , where
, where
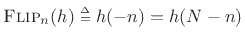 , i.e.,
, i.e.,
![$\displaystyle y(n) \eqsp \langle x, \hbox{\sc Shift}_n[\hbox{\sc Flip}(h)] \rangle.$](img1319.png) |
(9.14) |
This form describes graphical convolution in which the output
sample at time 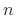 is computed as an inner product of the impulse
response after flipping it about time 0 and shifting time 0 to time
is computed as an inner product of the impulse
response after flipping it about time 0 and shifting time 0 to time
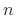 . See [264, p. 105] for an illustration of graphical
convolution.
. See [264, p. 105] for an illustration of graphical
convolution.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by a filter with impulse-response
by a filter with impulse-response ![]() to produce an
output signal
to produce an
output signal ![]() . By the convolution theorem for DTFTs
(§2.3.5),
. By the convolution theorem for DTFTs
(§2.3.5),
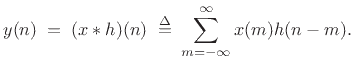
![]() , and
, and
![]() , where
, where
![]() , i.e.,
, i.e.,